그래프란?
- 연결되어 있는 객체 간의 관계를 표현하는 자료구조
- 객체를 나태내는 정점 또는 노드와 객체를 연결하는 간선 또는 링크의 집합
- 정점(vertax) : 여러가지 특성을 가질 수 있는 객체
- 간선(edge) : 정점들 간의 관계를 의미
-G = (V,E)로 표시, V는 그래프에 있는 정점들의 집합이며 E는 정점을 연결하는 간선들의 집합이다.

그래프의 종류
- 무방향 그래프( undirected graph ) : 두 정점을 연결하는 간선에 방향이 없는 그래프로 간선을 통해서 양방향 이동이 가능하다. 정점 A와 정점 B를 연결하는 간선을 (A,B)로 표현하고 (A,B) = (B,A)이다.

- 방향 그래프( directed graph ) : 간선에 방향이 있는 그래프로 간선을 통해서 한쪽 방향으로만 갈 수 있다(일반통행). 정점 A에서 정점 B를 연결하는 간선, A->B를 <A,B>로 표현하며 <A,B> != <B,A>이다.

- 가중치 그래프 ( weighted graph ) : 정점을 연결하는 간선에 비용이나 가중치, 길이가 할당된 그래프이다. 예를 들어 각 도시를 정점이라 하고 도시 연결도로를 간선이라 했을 때 간선에 길이나 비용(가중치)를 기입한 것이다.
G = (V, E, W)로 표현하며 V(G) 는 그래프 G의 정점들의 집합이며 E(G)는 그래프 G의 간선들의 집합이고 W(e)는 간선 e의 강도, 비용, 길이다.

- 완전 그래프( complete graph ) : 모든 정점이 연결되어 있는 그래프이다. 즉, 각 정점에서 다른 모든 정점을 연결하여 최대로 많은 간선 수를 가진 그래프이다. 정점이 n개인 무방향 그래프의 완전 그래프의 최대 간선의 수는 n(n+1)/2개이며
정점이 n개인 방향 그래프의 최대 간선의 수는 n(n-1)이다.

- 부분 그래프 (subgraph ) : 원래의 그래프에서 정점이나 간선을 일부만 제외하여 만든 그래프이다. 즉, 정점 집합 V(G)와 간선집합 E(G)의 부분 집합으로 이루어진 그래프이다.
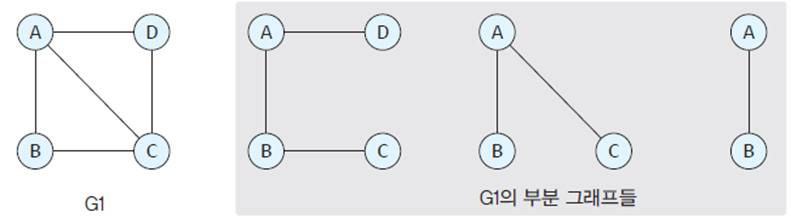
인접정점과 차수
- 인접정점( adjacent vertex )은 하나의 정점에서 간선에 의해 직접 연결된 정점이다.

- 차수(degree) : 하나의 정점에 연결되어 있는 다른 정점의 수로 정점에 부속되어 있는 간선의 수이다. 위의 사진에 무방향그래프에서 G1에서 정점 0의 차수는 3이고, 차수의 합은 간선의 수의 2배이다.
하지만 방향그래프에서는 진입 차수( in-degree )는 정점을 머리로 하는 간선의 수, 진출 차수( out-degree )는 정점을 꼬리로 하는 간선의 수, 전체 차수는 진입 차수 + 진출 차수이다. 모든 진입(진출) 차수의 합은 간선의 수이다.

그래프의 경로(path)
- 그래프에서 간선을 따라 갈 수 있는 길을 순서대로 나열한 것, 즉 정점 S에서 정점 E까지 간선으로 연결된 정점을 순서대로 나열한 리스트이다.
- 무방향 그래프의 정점 s로 부터 정점 e까지의 경로
정점의 나열 s, v1, v2, …, vk, e
반드시 간선 (s, v1), (v1, v2), …, (vk, e) 존재해야 함
무방향 그래프 G1에서 정점 A에서 정점 C까지는 A-B-C 경로와 A-B-D-C 경로, A-D-C 경로, 그리고 A-D-B-C 경로가 있음
- 방향 그래프의 정점 s로 부터 정점 e까지의 경로
정점의 나열 s, v1, v2, …, vk, e
반드시 간선 <s, v1>, <v1, v2>, …, <vk, e> 존재해야 함
- 경로의 길이(length) : 경로를 구성하는데 사용된 간선의 수
- 단순 경로(simple path): 경로 중에서 반복되는 간선이 없는 경우
- 사이클(cycle) : 단순 경로 중에서 경로의 시작 정점과 마지막 정점이 동일한 경우

- DAG(Direcred Acycle Graph): 방향 그래프이면서 사이클이 없는 그래프
- 연결 그래프(connected graph): 서로 다른 모든 쌍의 정점들 사이에 경로가 있는 그래프로 떨어져 있는 정점이 없는 그래프이다. 그래프에서 두 정점 A에서 B까지의 경로가 있으면 A와 B가 연결되어 있다 함
- 단절 그래프(disconnected graph): 연결되지 않은 정점이 있는 그래프
- 트리(tree) : 그래프의 특수한 형태로서 사이클을 가지지 않는 그래프
인접행렬이란?
- 간선의 집합을 2차원 배열을 사용해 표현
- 그래프의 두 정점을 연결한 간선의 유무를 행렬로 저장
- n개의 정점을 가진 그래프 -> n x n 정방행렬 이용, 행렬의 행번호와 열번호는 그래프의 정점이다.
- 행렬 값은 두 정점이 인접되어 있음 1, 아니라면 0이고 대각선 성분은 모두 0이다
- 무방향 그래프의 인접행렬 : 인접행렬의 대칭, 행 i의 합 = 열 i의 합 = 정점 i의 차수
- 방향 그래프의 인접행렬 : 행 i의 합 = 정점 i의 진출차수, 열 i의 합 = 정점 i의 진입 차수



- 간선의 수와 무관하게 항상 n^2개의 메모리 공간이 필요하기에 정점에 비해 간선의 수가 많은 그래프에 효율적
- u와 v를 연결하는 간선(u,v)의 유무는 인접행렬의 요소여서 adj[u][v]를 조사하면 바로 알 수 있어 O(1).
- v의 차수는 인접행렬에서 v에 해당하는 행의 모든 성분을 조사해야 하기에 O(n)
- v의 모든 인접 정점을 구하려면 해당 행의 모든 요소를 조사해야 하기에 O(n)
- 그래프의 전체 간선 수를 구하려면 인접 행렬 전체를 조사해야 하므로 O(n^2)




인접리스트란?
- 각 정점이 연결리스트를 가져서 각 정점에 대한 인접 정점들을 연결하여 만든 단순 연결리스트이다.
- 각 정점의 차수만큼 노드를 연결, 리스트 내의 노드들은 인접 정점에 대해 오름차순으로 연결
- 인접리스트의 각 노드는 정점을 저장하는 필드와 다음 인접 정점을 연결하는 링크필드로 구성
- 정점에 대한 인접 리스트의 헤드포인터는 정점 개수만큼 필요
- 그래프는 정점의 집합이므로 각 정점에 대한 헤드 포인터를 그룹으로 묶어서 포인터 배열로 구성함

- n개의 정점과 e개의 간선을 가진 무방향 그래프의 인접리스트에서
헤드 노드 배열의 크기 : n, 연결하는 노드의 수 : 2e, 각 정점에 헤드에 연결된 노드의 수 : 정점의 차수
- n개의 정점과 e개의 간선을 가진 방향 그래프의 인접리스트에서
헤드 노드 배열의 크기 : n, 연결하는 노드의 수 : e, 각 정점에 헤드에 연결된 노드의 수 : 정점의 진출 차수
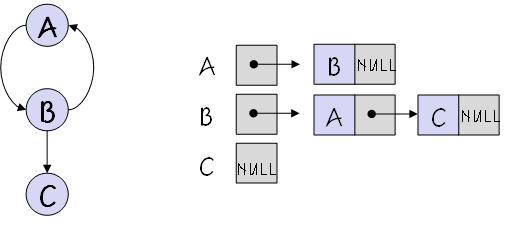
- n개의 연결리스트, 2e개의 노드 필요헤서 n + 2e개의 메모리 공간이 필요해 정점에 비해 간선의 수가 매우 적은 희소그래프에 효과적이다.
- 간선(u,v)가 있는지는 u의 연결리스트 전체를 조사해야 알 수 있다. 정점 u의 차수를 du라고 하면 O(du)
- v의 차수는 v의 연결리스트의 길이이므로 시간복잡도는 v의 차수에 비례. O(dv)
- 정점 v의 연결리스트의 모든 요소를 방문한다면 O(dv)
- 모든 인접 리스트의 요소를 방문하면 O(n+e)

그래프 탐색이란?
- 하나의 정점에서 시작하여 차례대로 그래프에 있는 모든 정점들을 한 번 씩 방문하여 처리하는 연산
- 많은 문제들이 단순히 그래프 탐색만으로 해결됨
- 탐색 방법 : 깊이우선탐색(DFS), 너비우선탐색(BFS)
깊이우선탐색(DFS)
- 시작 정점에서 출발하여 한 방향으로 갈 수 있는 경로가 있는 곳까지 깊이 탐색해 가다가 더 이상 갈 곳이 없다면, 가장 마지막에 만났던 갈림길 간선이 있는 정점으로 되돌아와 이곳으로부터 다른 방향의 간선으로 탐색을 계속 반복하여 결국 모든 정점을 방문하는 순회방법
- 가장 마지막에 만났던 갈림길 간선의 정점으로 가장 먼저 되돌아가면서 다시 깊이우선탐색을 반복해야 하므로 후입선출구조의 스택을 사용


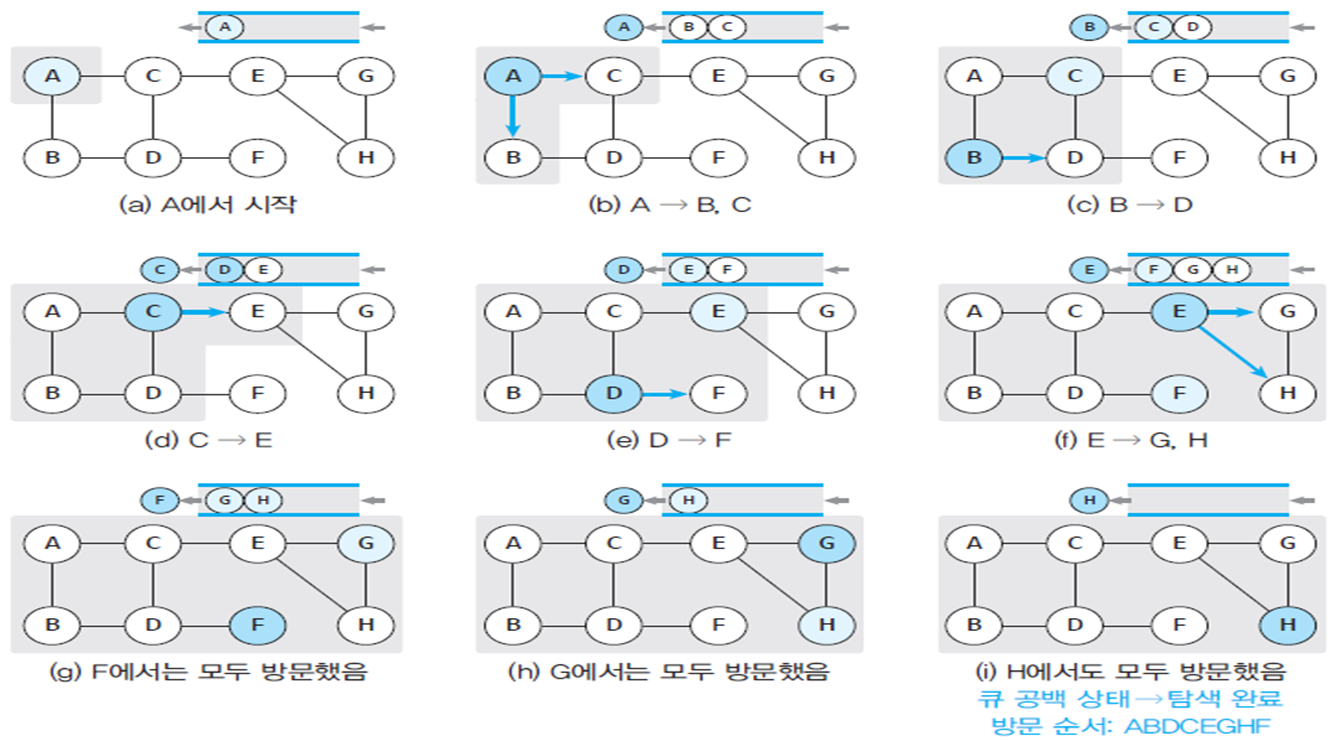
너비우선탐색(BFS)
- 시작 정점으로부터 가까운 정점을 먼저 방문하고 멀리 떨어져 있는 정점을 나중에 방문하는 순회방법
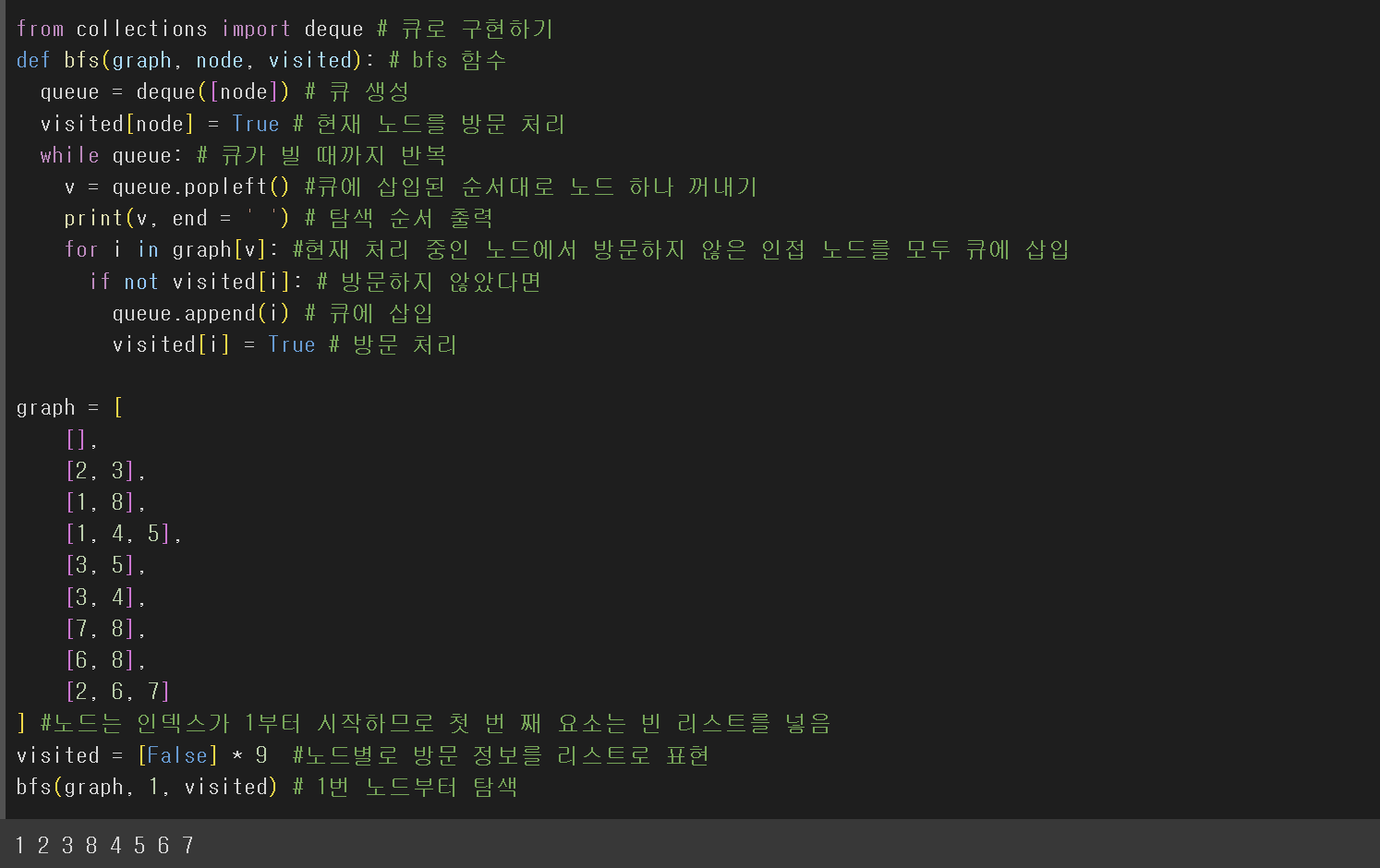
- 큐를 사용해 구현
신장트리(Spanning Tree)란?
- n개의 정점으로 이루어진 무방향 그래프 G에서 n개의 모든 정점과 n-1개의 간선으로 만들어진 트리
- 모든 정점들이 연결되어야 하고 사이클을 포함하면 안 됨
- 신장 트리는 n-1개의 간선을 가짐
- 최소의 링크를 사용하는 네트워크 구축시 사용(통신망, 도로망, 유통망 등)
- 다양한 신장트리 가능
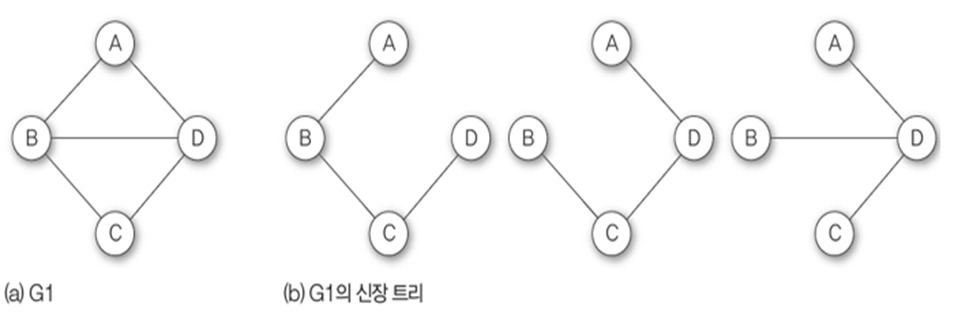
최소비용 신장 트리(Minimum cost Spanning Tree, MST)
- 트리를 구성하는 간선의 가중치 합이 최소인 신장트리
- 네트워크에 있는 모든 정점들을 가장 적은 수의 간선과 비용으로 연결
- 무 방향 가중치 그래프에서 신장 트리를 구성하는 간선들의 가중치 합이 최소인 신장 트리
MST의 응용
- 도로 건설 : 도시들을 모두 연결하면서 도로의 길이를 최소화
- 전기 회로 : 단자를 모두 연결하면서 전선의 길이를 최소화
- 통신 : 전화 케이블 망을 구성하면서 전화선의 길이 최소화
- 배관 : 배관을 모두 연결하면서 파이프의 총 길이를 최소화
- 통신망, 도로망, 유통망
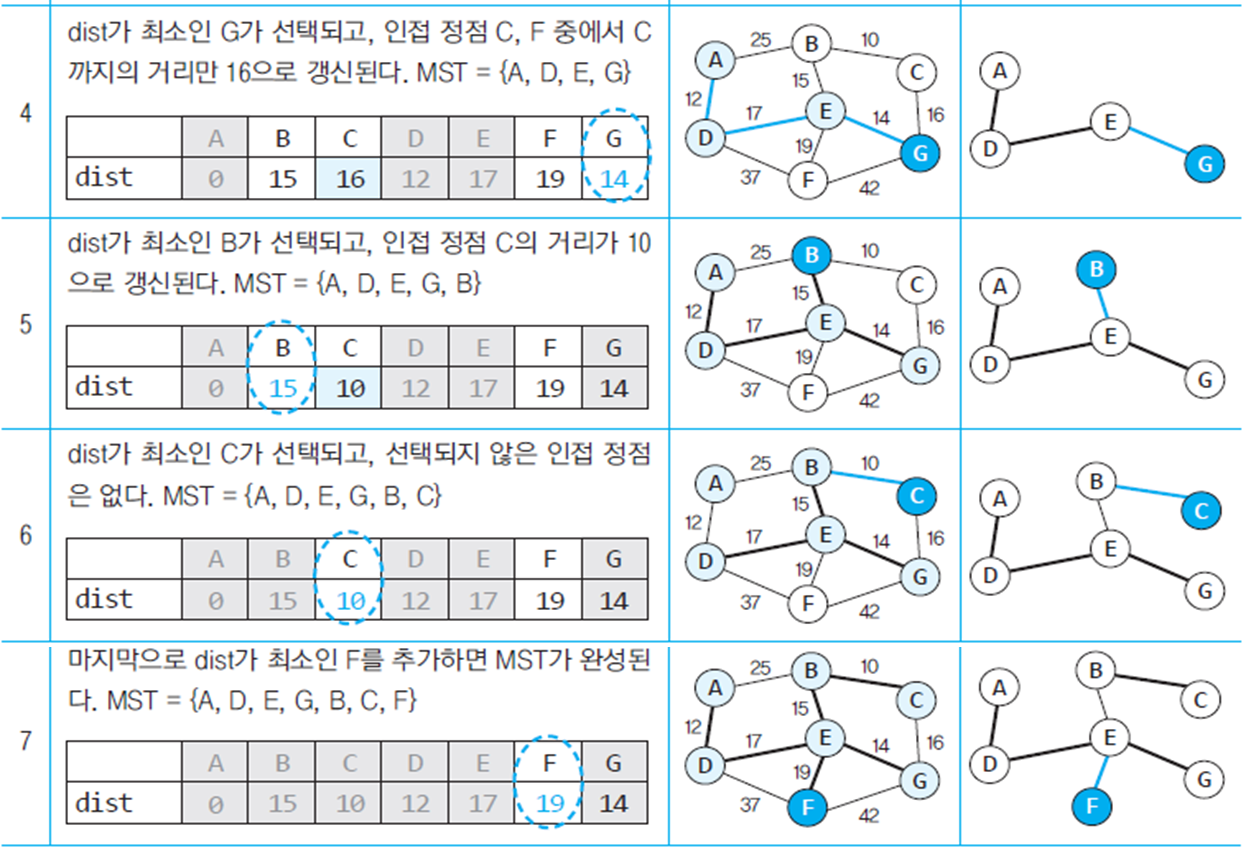
Prim의 MST 알고리즘
- 간선을 정렬하지 않고 하나의 정점에서부터 MST를 단계적으로 확장하는 방법
1) 처음에는 시작 정점만이 신장 트리 집합에 포함됨
2) 시작 정점부터 신장 트리 집합을 단계적으로 확장해 나감
3) 현재의 신장 트리 집합에 인접한 정점 중 최저 간선으로 연결된 정점 선택하여 신장 트리 집합에 추가
4) 이 과정을 n-1개의 간선을 가질 때까지 반복

- 밀접합 그래프에 유리하다.



Union, Find
- 서로소 집합 자료구조를 표시할 때는 기본적으로 트리 자료구조를 이용하는데 트리 자료구조는 계층을 가지고 있기에 노드들 간의 부모 - 자식 관계가 있음을 가정한다.
- 서로소 집합 정보(union 연산)가 주어졌을 때, 트리 자료구조를 활용해 집합을 표현하는 서로소 집합 계산 알고리즘은
1) Union(합집합) 연산 정보 중 1개를 확인하여, 서로 연결된 두 노드 A,B를 확인한다.
2) 두 노드 A, B 각각의 루트노드 A', B'를 알아낸다. (이 때, Find 연산을 수행하는 셈)
3) 보통은 A', B' 중 값이 작은 노드를 부모 노드라고 가정하고 연결시킨다. A' < B'라면 B' -> A'로 연결시킨다.(Union 연산을 수행하는 셈)
4) 나머지 Union 연산 정보를 순차적으로 받으면서 1~3과정을 반
Kruskal의 MST 알고리즘
- 사이클을 만들지 않는 가장 가중치가 작은 간선 n-1개를 순서대로 선택
- 사이클 검사 : union- find 알고리즘
- 대부분 간선들을 정렬하는 시간에 시간복잡도 좌우, 사이클 테스트 등의 작업은 정렬에 비해 매우 신속하게 수행
1) 주어진 모든 간선 정보에 대해 간선 비용이 낮은 순서(오름차순)으로 정렬
2) 정렬된 간선 정보를 하나씩 확인하면서 현재의 간선이 노드들 간의 사이클을 발생시키는지 확인
3) 만약 사이클이 발생하지 않는 경우, 최소 신장 트리에 포함시키고 사이클이 발생한 경우, 최소 신장 트리에 포함시키지 않음
4) 1번 ~ 3번 과정을 모든 간선 정보에 대해 반복 수




최단경로
- 신장트리가 아닌 가중치 그래프, 즉 네트워크에서 정점 u와 정점 v를 연결하는 경로 중에서 간선들의 가중치 합이 최소인 경로의 비용을 구하는 문제

가중치 인접 행렬
- 최단 경로를 구하려는 가중치 그래프의 가중치를 저장
- 그래프에서 사용한 인접 행렬과 같은 형태의 2차원 배열, 두 정점 사이에 간선이 없으면 0이 아니라 ∞(무한대) 값이 저장되어 있다고 가정.
- 각 정점은 자기 자신과 이어진 간선을 허용하지 않으므로 가중치 인접 행렬에서 대각선 값은 0

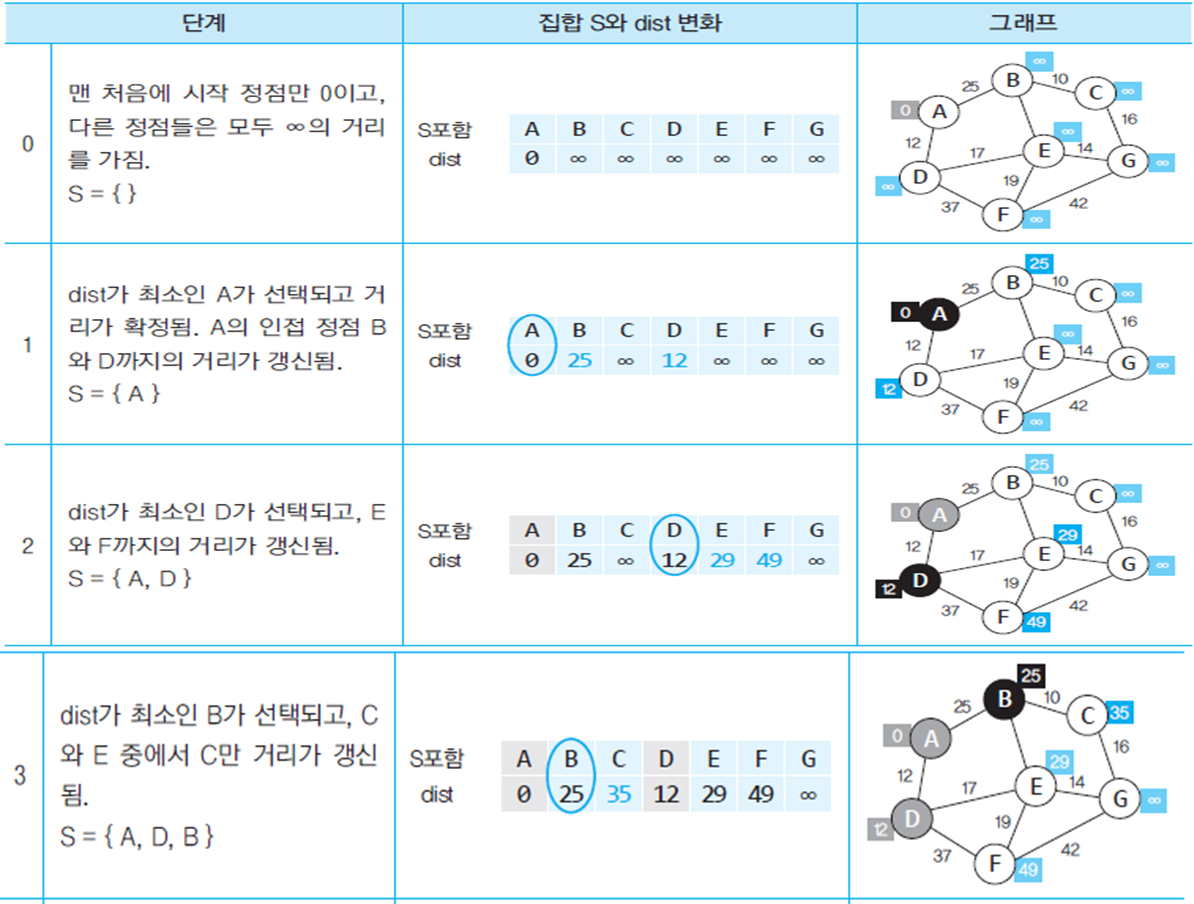
Dijkatra(다익스트라) 알고리즘
- 하나의 시작 정점에서 다른 모든 정점까지의 최단 경로를 구함
- 음의 간선이 없을 때 정상적으로 동작
- 그리디 알고리즘으로 분류 : 매 생황에서 가장 비용이 적은 노드를 선택해 임의의 과정을 반복




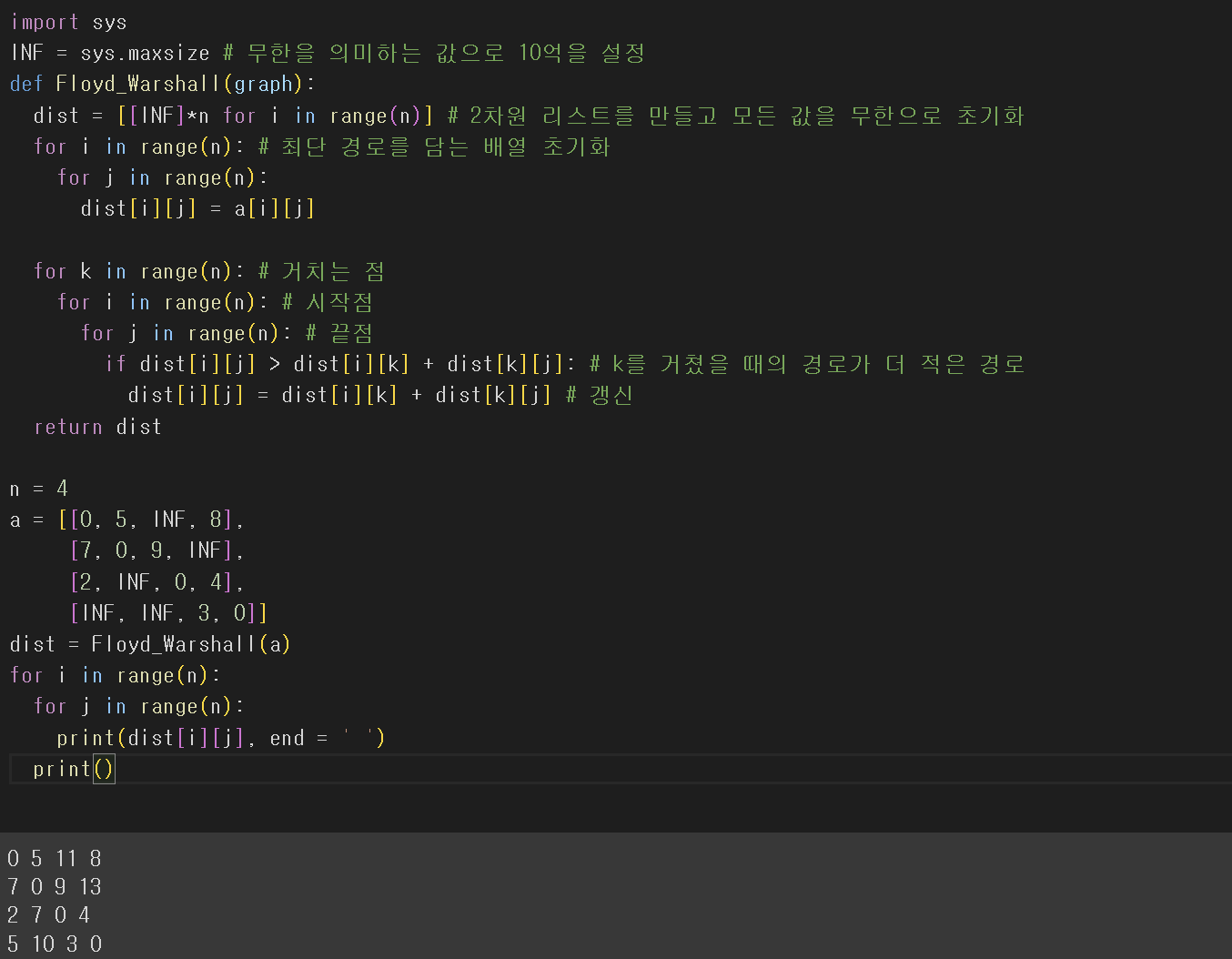
Floyd-Warshall(플로이드-워셜) 알고리즘
- 모든 정점 사이의 최단 경로를 한꺼번에 찾음
- 최단 경로 거리 행렬 A를 이용
- A^k[i][j]-> 0부터 k까지의 정점만을 이용한 i~j의 최단 경로 길이
- A^-1 -> A^0 -> A^1 -> ... -> A^n-1 순으로 최단 경로 구함
- A의 초깃값(A^-1)은 그래프의 인접행렬
- 삼중루프로 구성


내가 이해한 방식
1) 2차원 행렬로 표현, 정점 개수가 5면 5x5행렬로 만들고 인접 정점까지 거리표현 인접하지 않으면 정점은 무한대로 표기
2) A...G까지 하나하나 노드를 걸쳐가는 경우 최솟값으로 갱신, 즉
A^1은 A를 거쳐 가는 경우이다. A 노드를 걸쳐서 못가면 무한대로 표기하고 거쳐서 간다면 거리의 합으로 갱신.
A^2은 A를 걸치면서 B도 걸쳐서 가는 값이 존재하는가?를 판단하면 된다. 거서 가는 최촛값으로 갱신해야 함.
- 모든 정점 쌍의 최단 경로를 구하려면 다익스트라 알고리즘을 O(n^2)을 n번 반복해도 되며, 이 경우 전제 복잡도는 O(n^3)이 된다.
- 모든 정점 쌍의 최단 경로를 구하는데 있어 두 알고리즘 모두 동일한 O(n^3)의 복잡도를 가지지만 Floyd의 알고리즘은 매우 간별한 반복 구문을 사용하므로 다익스트라 알고리즘보다 효율적이다.
사진 출처:
쉽게 배우는 C 자료구조 | 생능출판사
코딩을 조금이라도 해 보았다면 프로그래밍이 자료(data)를 주로 다루는 것임을 알 수 있을 것이다. 우리가 프로그램을 개발할 때 가장 먼저 해야 할 일은 처리할 자료를 컴퓨터가 잘 다룰 수 있
www.booksr.co.kr
'자료구조' 카테고리의 다른 글
| 문자열 검색 (0) | 2024.08.02 |
|---|---|
| 재귀 알고리즘 (0) | 2024.08.02 |
| 트리 (0) | 2024.07.26 |
| 자료구조 - 연결리스트 (0) | 2024.07.19 |
| 자료구조 - 스택, 큐, 덱 (0) | 2024.07.09 |



