통계학이란?
- 자료의 수집과정을 설계하고, 자료를 요약하고 해석하여 결론을 이끌어 내거나 일반화하는 전체적인 원리와 방법론을 제공해주는 학문
- 자료를 효과적으로 수집, 합리적으로 해석하여 올바른 결론을 유도하는 과정
- 통계학의 영역은 자료의 수집과 조사를 통하여 사실을 밝혀내는 것을 포함하는 모든 지식의 습득과정까지 자연스럽게 확장된다.
다른 학문과 통계학의 공통점
- 새로운 정보나 지식을 얻기 위해서는 관련된 자료를 수집하여야 한다.
- 조건이 거의 같은 상황에서 관측되더라도 관측값들 사이에 어느 정도의 변동은 피할 수 없다. 예를 들어 같은 종류의 쥐들을 대상으로 약의 효능을 실험한다고 할 때 그 결과는 쥐마다 다르게 나오게 된다.
- 관련된 자료를 모두 수집한다는 것은 전혀 불가능하거나 현실적으로 있을 법하지 못한 경우가 흔하다.
- 관측과정을 통해서 실제로 수집하는 관측값과 주어진 상황에서 수집 가능한 모든 관측값과는 차이가 있다.
모집단과 표본
- 모집단이란 얻고자 하는 정보와 관련 있는 모든 개체로부터 얻을 수 있는 관측값들의 집합을 의미
- 표본은 모집단의 일부분으로, 원하는 정보를 얻기 위해 수행한 관측과정을 통하여 실제로 얻어진 관측결과의 집합
- 관측값은 사람이나 실험용 쥐 등으로부터 관측되거나 측정된 것이며, 여기서 사람과 쥐와 같은 개체는 표본추출단위임
통계학의 과제, 목표
- 통계학의 과제는 자료를 수집하고, 수집된 자료로부터 모집단에 대한 추론을 할 수 있도록 방법론을 제공해 주는 것이라고 할 수 있다.
- 목표는 관측값으로부터 효율적인 추론을 할 수 있도록 표본추출의 과정과 범위를 설계한 후에 표본에 포함되어 있는 정보를 분석해서 모집단에 관한 추론을 하는 것이다. 이때 추론에 수반되는 불확실성도 측정하는 것 또한 목표이다.
- 1차 목적 : 수집된 데이터를 요약하여 현상을 파악
- 2차 목적 : 데이터를 통해 얻어진 정보를 근거로 미지의 사실에대한 추론을 전개하여 합리적, 과학적, 객관적 의사결정 도출
통계학의 종류
- 기술통계학 : 수집된 자료를 숫자 또는 그래프로 정리, 요약하고 특징을 파악하는 분야(평균, 분산, 그래프 등)
- 추측통계학 : 표본정보를 이용하여 관심있는 전체 대상 집단인 모집단의 특성을 추측하는 분야(통계적추론)
- 수리통계학 : 통계학의 기본이 되는 수학적인 이론연구, 통계학의 이론적 근거를 수학적으로 정립
- 응용통계학 : 수리통계학에서 정립된 이론들을 바탕으로 실제 자료를 분석하는 방법을 연구하는 분야(설문조사, 환경 등)
- 모수통계학 : 모집단에 대한 분포를 가정하고 평균, 분산 등 모수에 대한 추론을 전개하는 일반적인 통계학
- 비모수통계학 : 모집단의 분포에 대한 가정이 어렵거나 표본 수가 적은 경우에 유용한 통계학
- 프리컨티스트통계학 : 관찰된 표본의 정보만을 사용하여 모수에 대한 추론을 전개하는 일반적인 통계학
- 베이지안통계학 : 모수를 확률분포로 고려하고, 표본정보와 모수에 대한 사전정보를 이용하여 모수에 대한 추론을 전개함, 표본의 정보에 연구자가 갖고있는 사전지식 또는 주관적의견/신념과 같은 정보도 포함하는 통계학, 조건부 확률 공식에 근거한다.
통계분석이란?
- 관심이 있는 집단(모집단)에서 추출된 표본을 대상으로 자료를 수집하여 모집단에 대한 정보를 얻고, 자료의 특성과 연구목적에 맞는 통계 분석 방법을 사용하여 합리적이고 과학적인 의사결정을 내리는 과정
- 일반적인 통계 분석 방법(프리컨티스트 통계학, 모수통계학)에서는 표본정보만을 사용
- 표본은 모집단의 특성을 골고루 잘 대표하도록 수집
조사의 종류
- 전수조사(총조사) : 인구 조사의 경우 사용되며 모집단을 구성하는 모든 개체들을 조사하여 데이터를 얻는 방법으로 전체를 모두 조사하는 것이기에 통계적 추론을 적용할 필요가 없지만 비용과 시간이 많이 소요됨.
- 표본조사 : 고비용 검사 또는 파괴검사(자동차 충돌, 찌그러짐), 고위험조사(치료제 개발) 등에서 사용되는 표본조사는 모집단 중 일부를 추출하여 모집단의 특성을 추론하며 전수조사에 비해 비용과 시간이 절감되지만 표본이 모집단을 잘 대표할 수 없을 때는 문제가 생길 수 있기에 표본의 대표성 확보가 필수임.
표본추출 방법
- 단순 랜덤 추출법 : 모집단의 원소가 n개일 때 각 원소에 1~n까지의 고유번호를 부여한 후, 필요한 표본의 수 k개를 랜덤하게 추출하는 방법으로 n이 충분히 크면 편향성이 존재하지 않지만 n이 작다면 편향성 문제가 존재
- 계통추출법 : n개의 표본을 원소의 개수가 N개인 모집단으로부터 추출할 때, N개의 원소를 k개씩(N/n) n개의 구간으로 나누고 각 구간에서 i번째를 차례대로 추출(10000개의 표본을 100개로 나누고, 구간이 그럼 100개임, 추출할 때 i = 33으로 정하게 되면 33, 133, 233,....으로 추출)
- 집락추출법 : 모집단이 동질적 집락으로 구성되어 있을 때, 먼저 집락을 임의로 선택한 후, 선택된 집락내에서 표본을 랜덤하게 추출(특정 기준으로 구역이 나뉜 구간을 뽑고 그 구간 안에서 동일한 비율로 추출)
- 층화추출법 : 모집단이 이질적 원소들로 구성된 경우, 먼저 이질적 모집단을 유사한 것끼리 몇 개의 층으로 나눈 후, 각 층에서 표본랜덤추출(조사 목적에 맞게 층분류 할 때 사용)
4가지 척도
- 명목척도(상호배타성) : 측정 대상이 어느 집단(범주)에 속하는지를 분류하는 경우에 사용되며 각 집단에 속하는 관측값의 도수를 세는 경우에 사용되는 척도, 숫자로 구별하여도 각 숫자 사이에는 크기의 차이나 우열의 차이가 없음(혈액형)
- 순서척도(계산불가) : 명목척도에 순서 정보를 추가하여 어떤 특성에 대한 측정 대상의 서열관계 측정(<,>,=), 서열에 따른 방향성이 있도록 측정하는 것이 바람직하다. (학력수준, 선호도조사)
- 구간척도 : 측정대상이 갖고있는 어떤 속성의 양을 측정하는 척도로 숫자로 측정되지만 절대원점(기준점)이 존재하지 않고 구간척도로 측정된 측정값의 비율은 전혀 의미가 없다. (온도가 0이라고 해서 온도가 없는 것이 아님, 곱, 나누기 불가)
- 비율척도 : 구간척도와 같이 숫자로 측정되지만 절대 원점이 존재하는 척도로 일반적인 숫자의 의미와 동일, 수학적 사칙연산이 그대로 적용된다.
자료의 형태
- 수치형 자료(양적자료) : 관측된 값이 수치로 측정되는 자료를 뜻하며 키, 몸무게와 같이 관측 가능한 값이 연속적이면 연속형자료라 하며 관측 가능한 값이 셀 수 있으면 이산형자료라고 한다.
- 범주형 자료(질적자료) : 관측 결과가 몇 개의 범주 또는 항목의 형태로 나타나는 자료이며, 각 범주에 속한 관측 값의 개수가 보통 관심의 대상이 된다. 범주 간에 순서의 의미가 있으면 순위형 자료라 하며 순서의 의미가 없으면 명목형 자료라 한다.
- 보통 관측값의 종류가 적은 경우에는 범주형 자료를 요약하는 기법을 사용하고 관측 값의 종류가 많은 경우에는 연속형 자료를 요약하는 기법을 사용하게 된다.
- 이산형 자료는 수치형자료로서 관측값의 크기가 의미가 있으므로 파레토그림과 같이 범주의 순서가 바뀌는 기법은 피해야 한다.
- 변수 : 관측되는 특성으로 수치형변수, 범주형 변수, 연속형 변수, 이산형변수, 순위형 변수, 명목형 변수가 있다.
범주형 자료의 요약
이산형자료도 아래의 여러 방법으로 표현이 가능하다
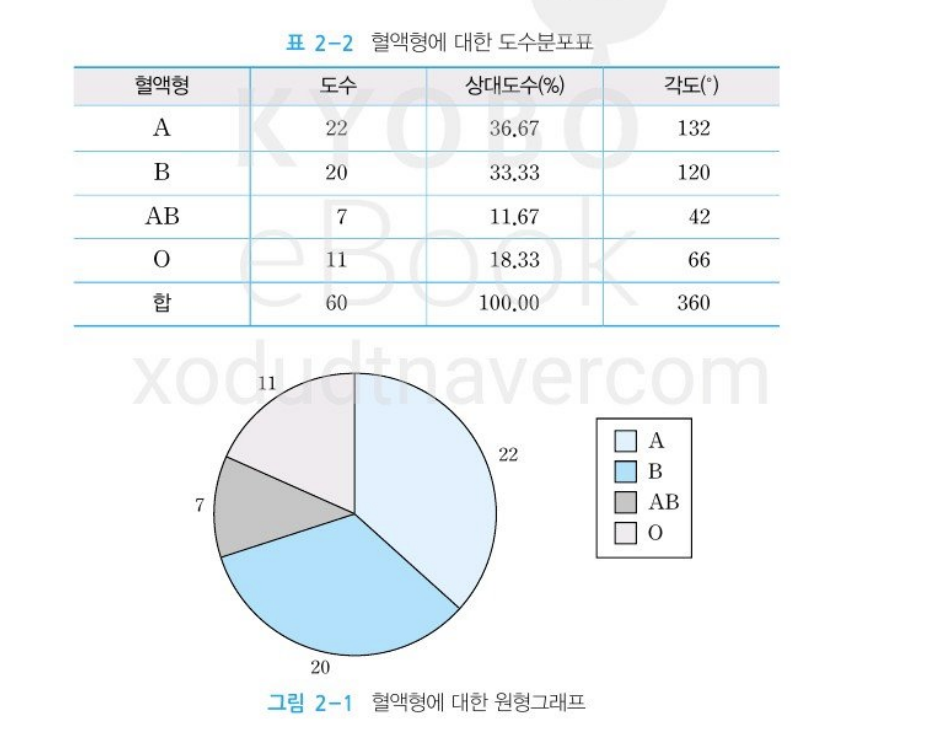
도수분포표
- 관측값의 개수를 그 범주의 도수라 하며 이 도수를 자료의 전채 개수로 나눈 비율을 그 범주의 상대도수라고 하는데 범주형 자료에서 범주와 그 범주에 대응하는 도수와 상대도수를 나열하여 표를 작성한 것을 도수분포표라 한다.
- 첫번째 열에 모든 범주를 나열하고, 두번째 열과 세번째 열에 각 범주에 상응하는 도수와 상대도수를 나열한다.

원형그래프
- 원을 먼저 그리고 이 원을 상대도수에 비례하도록 중심각을 나누어 마치 파이의 조각을 나눈 것과 같은 형태를 갖도록 하는 그림
- 전체에서 각 범주 또는 몇 개의 범주가 전체에서 차지하는 비율을 파악하기쉽다
- 범주 간의 도수를 비교하거나 도수 크기의 차이를 파악할 때 원형그래프를 이용하면 그 내용을 명확이 파악하기 힘든 경우가 많아 도수 또는 상대도수를 기입하기도 한다.
- 각도는 전체 각도가 360도이므로 360 x (각 변수의 상대도수)가 된다.
막대그래프
- 각 범주에서 도수의 크기를 막대로 그려 나타낸다. 즉 그래프의 한 축에는 도수에 대한 눈금을 그리고, 또 다른 축에는 범주를 나열한 후에 각 범주에 대하여 도수의 크기만큼 막대를 그리면 막대그래프가 된다.
- 각 범주가 차지하는 비율을 알기 위해서는 도수 대신 상대도수를 이용하는데 이때에는 왼쪽 수직 축에는 도수를, 오른쪽 수직 축에는 상대도수를 기록하기도 한다.
- 각 범주 간의 도수를 비교하는데 용이하지만 각 범주 또는 몇 개의 범주가 전체에서 차지하는 비율을 파악하려면 원형그래프가 적당하다.

파레토그림
- 명목형 자료에서 다수를 점유하고 있는 중요한 소수의 범주를 찾는데 파레토그림이 사용된다.
- 막대그래프의 일종으로, 상대도수의 크기가 큰 순서로 범주를 왼쪽부터 오른쪽으로 배열하여 만들어 가장 큰 막대가 왼쪽, 작은 막대가 오른쪽에 오도록 배열한다.
- 크기 순서대로 배열된 범주에서 누적상대도수를 구하여 그림에서 누적도수를 각 범주의 막대 위에 중앙에 표시하고 그 점들을 연결함으로써 상대도수가 증가하는 정도와 큰 도수의 범주들이 차지하는 비율을 쉽게 파악할 수 있다.
- 어떠한 범주가 중요한 범주인지 쉽게 파악이 가능해 문제 파악의 수단으로 많이 사용된다.


연속형 자료의 요약
점도표
- 연속형 자료에서 관측값의 개수가 상대적으로 적은 경우(20 또는 25이하) 점도표를 이용하여 자료 전체의 개요 파악
- 모든 자료를 나타낼 수 있도록 먼저 수평선을 긋고 눈금을 표시한 후 각 관측값에 해당되는 위치에 점을 찍어 표시하면 된다. 만약 해당되는 위치에 이미 점이 표시되어 있으면 그 점 위에 점을 표시하여 점도표를 그린다.

- 관측값의 개수가 많은 연속형 자료를 점도표로 나타내는 것은 고되며 때때로 점들이 뭉쳐 있어 알아보기도 힘들다.
이러한 경우 개개의 관측값을 그대로 사용하기보다는 자료를 크기에 따라 몇 개의 묶음으로 묶어 분석 -> 효율적
도수분포표
- 연속형자료에서는 모든 관측값을 포함하는 범위를 몇 개의 구간으로 나누어 각 구간에 포함되는 관측값의 개수(도수)를 세어 도수분포표를 작성
- 나뉘어진 각 부분을 계급, 각 계급에 포함되는 값의 범위를 계급구간, 각 계급구간의 크기를 계급구간의 폭이라 함
작성방법
1) 자료의 범위 : 자료에서 최댓값과 최솟값을 찾아 자료의 범의(range : 최댓값 - 최솟값)를 구한다.
2) 계급구간의 폭 : 계급의 개수가 5개~15개 정도 되도록 대략 정하고 자료의 범위를 구간의 개수로 나누어 얻은 값보다 조금 큰 값을 계급구간의 폭으로 정한다.
3) 계급구간 : 모든 관측값을 포함하도록 각 계급구간의 경계점을 구한다.
4) 도수 : 각 계급구간에 속하는 관측값의 개수를 세어 계급의 도수를 구한다.
5) 상대도수 : 각 계급의 도수를 전체 관측값의 개수로 나누어 계급의 상대도수를 구한다.


히스토그램
- 도수분포표를 기초로 하여 각 계급에 대하여 범주형 자료에서의 막대그래프와 같은 모양의 그림을 그릴 수 있는데 이를 히스토그램이라 함
- 각 계급구간 간의 도수를 비교가 가능하며 계급구간에 따른 도수 변화의 경향, 즉 자료의 분포를 알 수 있다.
- 계급구간과 막대의 높이가 주어짐으로써 그릴 수 있으며 막대의 높이는 상대도수를 계급구간의 폭으로 나눔으로써 구할 수 있다. 이 때 히스토그램의 전체 면적은 1이다.
- 모든 계급구간의 폭이 같으면 도수 또는 상대도수를 막대의 높이로 사용하여 그린 그림과 히스토그램은 같은 모양이 되어 도수나 상대도수를 막대의 높이로 사용하여 히스토그램의 모양을 얻기도 한다.
- 계급구간의 폭이 일정하지 않은 경우에는 계급구간에서 도수의 밀도에 따라 높이를 결정해야 하므로 상대도수를 계급구간의 폭으로 나눈 값을 막대의 높이로 사용하여야 한다.
- 가능하다면 항상 상대도수를 계급구간의 폭으로 나눈 값을 막대의 높이로 사용하는 것이 안전하다.
- 관측값의 개수 또는 계급구간의 폭이 다른 여러 개의 히스토그램을 비교할 경우 관측값의 개수나 계급구간의 폭에 영향을 받지 않도록 상대도수를 계급구간의 폭으로 나눈 값을 막대의 높이로 사용하는 것이 바람직하다.



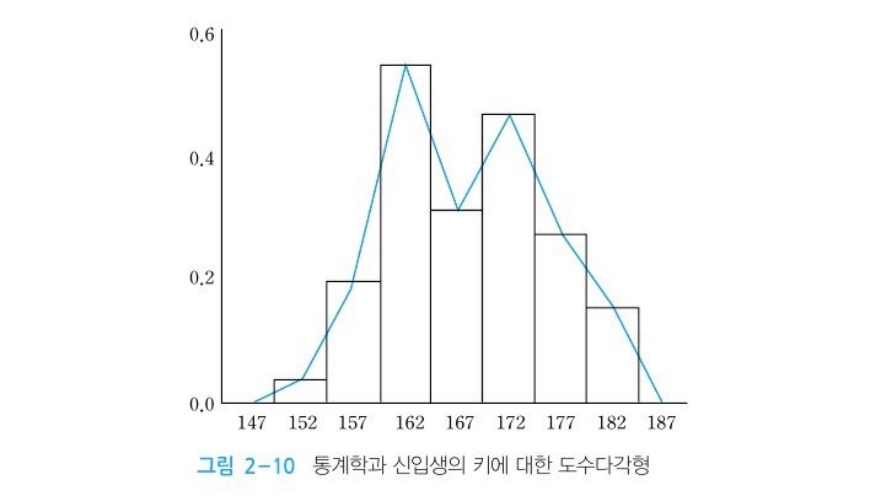
도수다각형
- 히스토그램에서 각 계급구간의 막대 상단의 중앙점을 직선으로 연결하여 그린다.
- 관측값의 집중된 위치, 집중된 정도, 치우친 정도, 꼬리의 두터움 등 분포의 상태를 쉽게 파악 가능
- 여러 개의 자료를 비교하는 데도 유용하게 쓰임

줄기-잎 그림
- 히스토그램이나 도수다각형은 자료의 분포를 쉽게 파악할 수 있게 하지만 개개의 관측값에 대한 정보를 잃어버리게 되는데 이 때 자료의 분포를 시각적으로 쉽게 파악하면서 각 관측값을 유지하는 방법으로 줄기-잎 그림이 사용된다.
줄기-잎 그림의 작성
1) 관측값을 보고 앞 단위와 뒷 단위를 정한다.
2) 앞 단위를 줄기로 하여 순서대로 세로로 배열하고 그 옆에 수직선을 그린다.
3) 뒷 단위를 잎으로 하여 해당하는 관측값을 앞 단위 오른쪽에 가로로 기입한다.
4) 각 줄기에서 잎 부분의 값을 작은 숫자가 왼쪽에 오도록 크기 순서로 재배열한다.

- 순서대로 배열된 관측값의 장점과 히스토그램의 장점을 모두 가지고 있다.
- 최댓값, 최솟값, 특정 관측값의 위치 등을 쉽게 파악할 수 있으며 그리기가 쉬워 자주 사용된다.
- 그러나 관측값의 개수가 많은 경우 제한된 공간에 그리는 것이 불가능 할 수 있으며 각 관측값이 지나치게 흩어져 있는 경우에는 줄기-잎그림보다는 히스토그램 또는 도수다각형을 사용하는 것이 좋다.
분포의 모양
- 대칭형분포 : 그림 좌우의 모양이 중앙을 기준으로 비슷하다. 여기에 속하는 (a)의 분포와 같이 중앙에 관측값이 몰려 있고 중앙에서 멀어질수록 도수가 줄어드는 대칭형 분포를 종모양의 분포가 있고 (b)의 분포는 봉우리가 2개이고 이러한 분포는 두 개의 다른 집단이 같이 섞여 있을 때 사용되는 이봉형분포가 있으며 (c)와 같이 사각형 모양을 가진 관측값이 모든 계급 구간에 고르게 나타나는 균일형 분포가 있다.
- 편중된 분포 : 관측값이 한쪽에 몰려 있는 분포이며 오른쪽으로 편중, 왼쪽으로 편중되었다고 칭하며 영어표현에서는 방향이 바뀌는 것이 유의해야 한다.

사진 출처
https://product.kyobobook.co.kr/detail/S000060624898
통계학: 파이썬을 이용한 분석 | 인하대학교 통계학과 - 교보문고
통계학: 파이썬을 이용한 분석 | 오늘날 통계학을 이용한 데이터 분석에서 통계소프트웨어의 사용은 거의 필수적이다. 파이썬(Python)을 이용하여 실습과 분석을 할 수 있도록 설명한 책이다. 파
product.kyobobook.co.kr
'통계학' 카테고리의 다른 글
| 정규분포 (0) | 2025.03.23 |
|---|---|
| 이항분포와 그와 관련된 분포들 (1) | 2025.03.20 |
| 확률분포 (0) | 2024.07.30 |
| 두 변수 자료의 요약, 확률 (2) | 2024.07.26 |
| 수치를 통한 연속형 자료의 요약 (0) | 2024.07.21 |




