두 변수 자료의 요약, 확률
분할표란?
- 도표로 요약된 자료
- 필요(목적)에 따라 여러 가지 값을 교차하는 부분에 표시할 수 있는데, 그 중 하나가 상대도수

산점도란?
- 두 변수의 경우에도 그림을 통하여 두 변수 간의 관계를 파악할 수 있는데 이 때 사용되는 그림이 산점도
- 두 변수는 서로 관계가 있을까? 관계가 있다면 두 변수가 어떤 관계가 있다고 할 수 있을까?와 같이 두 변수의 연관 관계에 대하여 알고 싶다면 두 변수를 동시에 고려할 필요가 있는데 두 변수 x와 y간의 관계를 분석할 때 중요한 첫 번째 단계가 자료에 대한 그림을 그리는 것이다. 변수 x를 수평축에 놓고 변수 y를 수직축에 놓은 후에 각 관측값의 짝을 좌표 위에 표시함으로써 얻게 되는 그림이 산점도이다.

표본상관계수란?
- 산점도를 통하여 두 변수 사이의 관계를 시각적으로 파악할 때 많은 경우에 점들이 띠를 형성하듯이 몰려 있게 되는데 이 때 띠의 형태는 직선, 곡선 등 여러 형태를 가질 수 있지만 여기서 가장 관심이 있는 경우는 직선의 형태로 산점도에서 점들이 얼마나 직선에 가까운가의 정도를 나타내는데 쓰이는 척도

표본상관계수의 특징
1) 표본상관계수 r은 항상 -1과 1사이에 있다.
2) 표본상관계수의 절댓값의 크기는 직선관계에 가까운 정도를 나타내고 표본상관계수의 부호는 직선관계의 방향을 나타내는데 구체적으로
- r > 0 : 산점도에서의 점들이 좌하에서 우상 방향으로 띠를 형성한다. 즉 한 변수의 값이 작으면 다른 변수의 값도 작고, 한 변수의 값이 크면 다른 변수의 값도 큰 경향을 가지고 있어 하나의 직선으로 나타냈을 때 그 직선의 기울기는 양수가 된다.
- r < 0 : 산점도에서의 점들이 좌상에서 우하 방향으로 띠를 형성한다. 즉 한 변수의 값이 작으면 다른 변수의 값은 크고, 한 변수의 값이 크면 다른 변수의 값은 작은 경향을 가지고 있어 이러한 경향을 하나의 직선으로 나타냈을 때 그 직선의 기울기는 음수가 된다.
- r = 1 : 모든 점이 정확히 기울기가 양수인 직선 위에 위치
- r = -1 : 모든 점이 정확히 기울기가 음수인 직선 위에 위치
표본상관계수의 절댓값이 클수록, 즉 표본상관계수의 값이 1 또는 -1에 가까울 수록 점들은 기울기가 양수 또는 음수인 직선에 가깝게 몰려 있다는 것을 나타낸다. 또한 표본상관계수가 0에 가까울수록 두 변수 간에 직선의 관계가 매우 약함 의미
3) 표본상관계수의 단위는 없다. 표본상관계수의 식에서 변수 x의 단위와 변수 y의 단위는 분모와 분자에서 상쇄되어 없어진다. 따라서 표본상관계수를 이용하여 단위가 다른 여러 쌍의 변수에서 직선관계의 정도를 비교할 수 있다.

상관관계와 인과관계
- 자료분석 시 주의해야 할 것은 큰 상관계수값이 항상 두 변수 사이의 어떤 인과관계를 의미하지는 않는다는 사실이다.
- 예를 들어 크기가 아주 다른 몇 개의 도시에서 매월 발생한 살인사건의 발생건수 (x)와 종교집회의 횟수(y)를 조사하여 산점도를 작성하였다 하자. 이 자료는 아마도 +1에 가까운 표본상관계수를 가질 것이다. 두 변수 사이의 인과관계가 성립된다면 살인사건 발생을 줄이기 위하여 종교집회를 억제하면 된다는 결론을 얻게 되지만 우리가 간과한 사실은 주민의 수가 많은 큰 도시에서는 살인사건도 많고 종교집회도 많지만, 주민의 수가 적은 도시에서는 살인사건과 종교집회 모두 적은 편이라는 사실이다. 따라서 두 변수의 높은 상관계수의 값은 주민의 수에 따른 결과이지 결코 두 변수 사이의 높은 인과관계를 나타내는 것은 아니라는 것을 알 수 있는데 이때 주민의 수와 같은 변수를 잠재변수라 한다.
- 어떤 두 변수가 진짜로 인과관계가 있는지 아니면 연관성만 높은것인지를 결정하는 것은 통계적인 추론보다는 두 변수 사이의 연관성에 대한 이해나 그 분야에 대한 전문적인 해석이 필요하다.
사건의 확률이란?
- 한 사건의 확률이란 그 사건이 일어날 가능성의 정도를 나타내 주는 수치이다. 즉 실험이나 관측의 결과로서 나타날 수 있는 상황이 일정하지 않을 때 그 불확실성을 설명하기 위해 확률이 이용된다.
- 동일한 조건하에서 한 가지 실험을 반복할 때 전체 실험 횟수에서 그 사건이 일어나리라고 예상되는 횟수의 비율을 뜻하기도 하며 사건을 A라고 하면 사건 A의 확률을 P(A)로 표기한다.
- 위에서 언급한 실험이란 일반 연구 실험실에서 행해지는 것만이 아니라 동전던지기나 여론조사 등 다양한 결과가 예측되는 행위일체를 뜻한다.
- 시행은 정해진 실험을 한 번 수행하거나 조사를 한 번 실시하는 것으로 우연이 지배하는 사건의 결과를 관찰하는 과정이다.
- 표본공간(sample space) : 한 실험에서 나올 수 있는 모든 결과들의 모임( 사건이 가질 수 있는 결과 값, 동전 앞면은 앞,뒤의 결과만 나온다)
- 근원사건(elementary outcomes) : 표본공간을 구성하는 개개의 결과
- 사건(event) : 표본공간의 부분집합으로 어떤 특성을 갖는 결과들의 모임(즉, 근원사건들의 집합)
- 연속표본공간(continuous sample space) : 표본공간의 원소가 연속체로 주어져 나열할 수 없는 경우

확률의 해석방법
- 확률의 고전적 정의 : 확률은 실험과 사건의 정의로부터 객관적으로 파악 가능하다. 즉 실험과 사건의 정의로부터 누구나 동일한 확률값을 얻을 수 있다.
수학자 라플라스는 어떤 사건이 발생 확률을 표본공간의 원소의 수와 특정 사건에 속하는 수의 비로 정의했다. 또한 안에 있는 원소들의 발생 가능 확률이 모두 동일하다 가정해야 한다.
- 확률의 상대도수에 의한 해석 : 독립적으로 반복되는 실험에 의하여 나타난 결과를 확률로 표현, 즉 실험을 독립적이고 객관적으로 무한 반복하여 실험자의 주관이 개입되지 않은 객관적 확률을 얻을 수 있다는 것으로 확률의 상대도수에 의한 해석을 통해 구해지는 확률을을 객관적 확률이라 한다. 이론적인 값이 존재하지 않는 경우에 적용하는 것이 더 현실적이다.
- 확률의 주관적 해석 : 주관적이라는 사전적 의미가 그대로 적용되는 확률로 동일한 사건의 발생확률을 각자 다르게 고려한다.
확률의 계산 규칙
- 규칙1(균일확률) : 표본공간은 k개의 원소로 이루어져 있고 각 근원사건이 일어날 가능성이 동일하다고 할 때 근원사건 중 하나가 일어날 확률을 1/k로 주어진다. 또 사건 A가 m개의 근원사건으로 이루어져 있다면 사건 A가 일어날 확률은 아래 그림과 같다.

- 규칙2(상대도수 수렴치로서의 확률) : 동일한 실험을 N회 반복할 때 사건 A의 상대도수는 아래 그림과 같이 표현된다

여기서 만약 N이 증가함에 따라 상대도수가 일정한 값으로 수렴한다면, 그 값으로 사건 A가 일어날 확률 P(A)를 추정.
- 여사건 : 사건 A의 여사건은 A에 포함되지 않은 근원사건들의 모임으로 A^c로 표현.
- 합사건 : 사건 A,B의 합사건은 A 혹은 B에 포함되는 근원사건들의 모임으로 A U B로 표현.
- 곱사건 : 사건 A,B의 곱사건은 A와 B에 동시에 포함되는 근원사건들의 모임.
- 배반사건 : 동시에 일어날 수 없는 사건
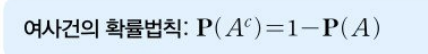
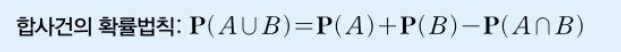
집합이란?
- 어떤 조건에 따라 결정되는 원소들의 모임
- 개념이 정확하게 정의된 원소들의 모임
- 집합에 속학 원소의 개수에 따라 유한집합/무한집합으로 구분
- 유한집합 : 원소의 개수를 셀 수 있는 집합 ex) {1,2,3,4,5}
- 무한집합 : 원소의 개수를 설수 없는 집합 ex) {x| 0<x<2}
- 공집합 : 원소가 없는 집합, 모든 원소의 부분집합
- 부분집합 : 어떤 집합의 일부분으로 구성되는 집합
- 합집합 : 두 집합 A와 B중 하나의 집합에라도 속하는 원소들로 구성된 집합
- 교집합 : 두 집합 A와 B에 모두 속하는 원소들로 구성된 집합
- 차집합 : 두 집합 중 하나에만 속하는 원소들로 구성된 집합
- 여집합 : 집합 A가 전제 집합 S의 부분집합일 때, A의 여집합은 전제 집합 S의 원소들 중에서 A에 속하지 않는 원소들로 구성된 집합
- 배반집합 : 두 집합 A와 B에 교집합이 존재하지 않는 경우이다.
조건부확률이란?
- 사건 B에 관한 정보(사전정보)가 주어졌을 때 사건 A의 교정된 확률을, B가 주어졌을 때 사건 A의 조건부확률이라함.

- 위를 통해 곱사건의 확률법칙을 구하면 아래의 사진과 같다.

- 두 사건이 독립이라면


- 만약 두 사건의 확률이 모두 양수라면 독립과 배반의 조건을 동시에 만족시킬 수 없다.

- 곱사건의 확률법칙과 사건의 분할을 이용하여 임의의 사건을 확률을 표현하는 것을 총확률의 법칙(전확률정리)이라 한다.


- 결론이 주어지고 원인을 추적할 때 사용하며, 조건부 확률의 앞뒤 순서를 변형해서 표현이 가능하다.
사진 출처:
https://product.kyobobook.co.kr/detail/S000060624898
통계학: 파이썬을 이용한 분석 | 인하대학교 통계학과 - 교보문고
통계학: 파이썬을 이용한 분석 | 오늘날 통계학을 이용한 데이터 분석에서 통계소프트웨어의 사용은 거의 필수적이다. 파이썬(Python)을 이용하여 실습과 분석을 할 수 있도록 설명한 책이다. 파
product.kyobobook.co.kr
