트리
트리란?
- 원소들 간에 계층적인 관계를 나타내는 계층형 자료구조
- 원소들 간에 1:n 관계를 가지는 비선형 자료구조(순서가 존재)
- 상위 원소에서 하위 원소로 내려가면서 확장되는 트리모양 구조
- 가계도, 컴퓨터 폴더구조, 탐색과 힙의 결정트리에 사용
- N-링크/ 자식-형제 표현법
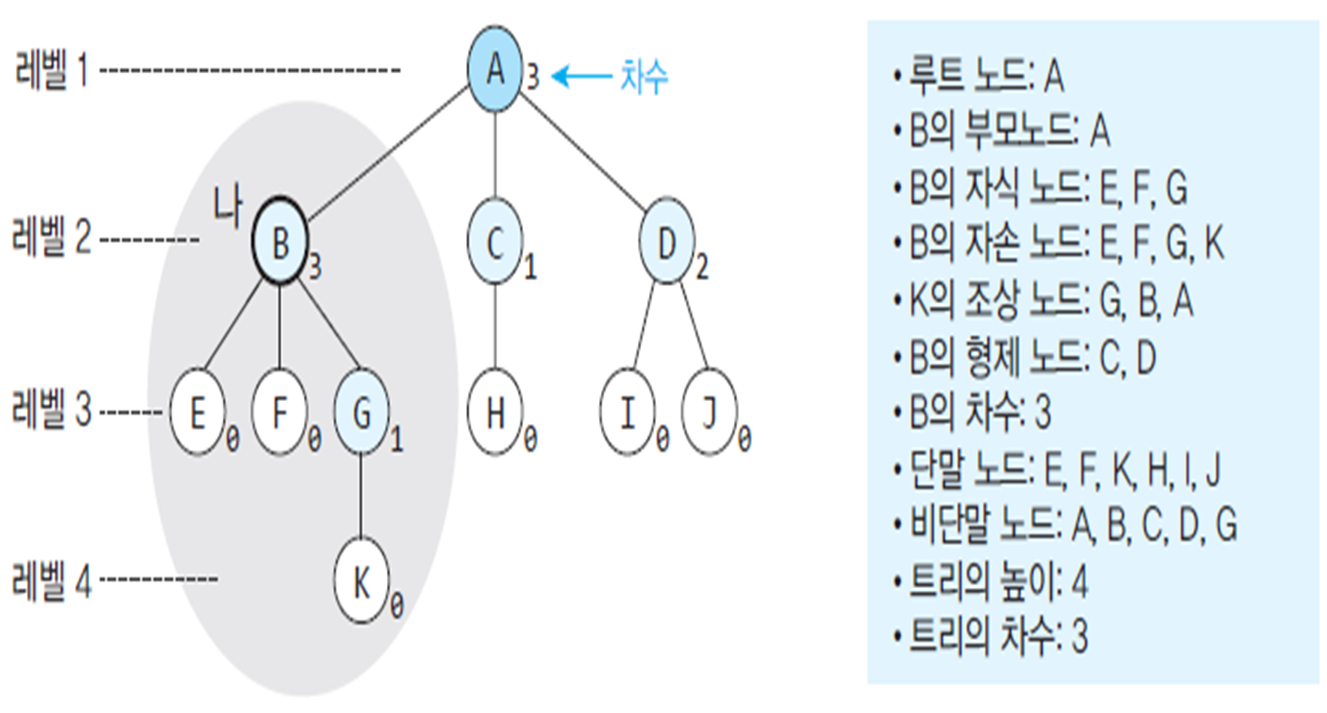
트리용어
- 노드(node) : 트리의 구성요소
- 간선(edge) : 노드를 연결하는 선 (부모 - 자식)
- 루트(root) : 부모가 없는 노드, 최상위 노드
- 서브트리(subtree) : 하나의 노드와 자손들로 이루어짐(루트를 제외한 나머지 노드들)
- 단말노드(terminal node) : 자식이 없는 노드
- 비단말노드(nonterminal node) : 자식이 있는 노드
- 조상노드(ancesor node) : 간선을 따라 루트노드까지 경로에 있는 모든 노드
- 형제노드(sibling node) : 같은 부모 노드의 자식 노드들
- 차수(degree) : 노드의 자식 노드수
- 노드의 차수 : 노드에 연결된 자식 노드의 수
- 트리의 차수 : 트리에 있는 노드의 차수 중에서 가장 큰 값
- 레벨 : 트리의 각 층의 번호
- 높이 or 깊이 : 트리의 최대 레벨
- 노드의 높이 : 루트에서 노드에 이르는 간선의 수, 즉 노드의 레벨
- 트리의 높이 : 트리에 있는 노드의 높이중에서 가장 큰 값, 즉 최대 레벨
- 숲(forest) : 서브트리의 집합, 트리에서 루트노드를 제거하면 서브트리들로만 생기는 집합
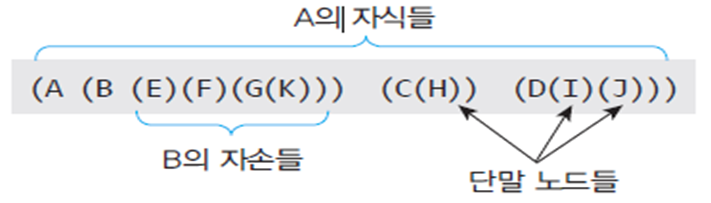
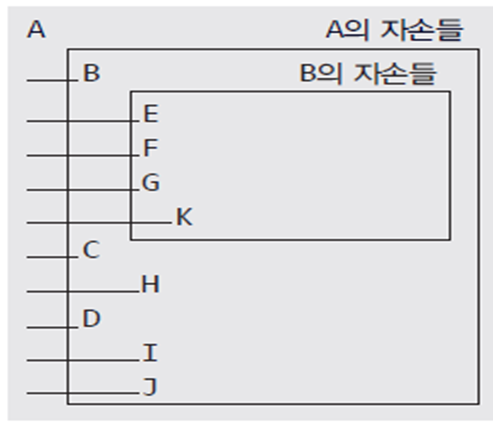
트리의 다른 표현 방법
- 중첩된 집합, 중첩된 괄호, 들여쓰기

이진트리란?
- 모든 노드가 2개의 서브트리를 가지고 있는 트리
- 트리의 모든 노드의 차수(자식의 수)를 2이하로 제한하여 전체 트리의 차수가 2이하가 되도록 정의한 트리
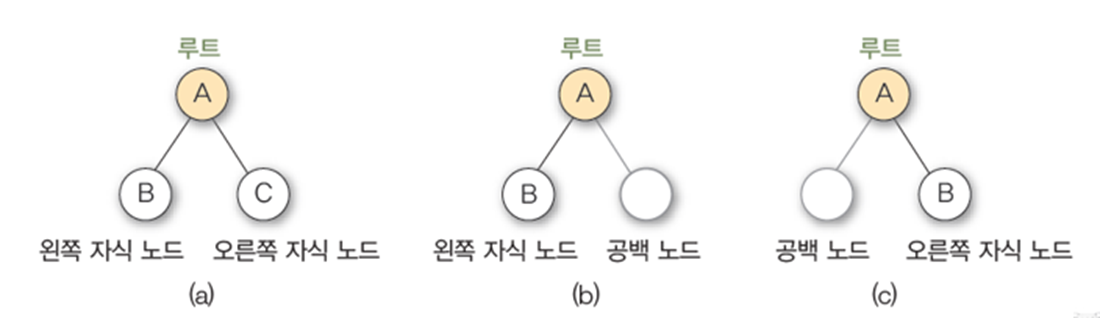
- 왼쪽 자식과 오른쪽 자식은 반드시 구별해야함
- 노드의 차수 최대 2 => 왼쪽 자식과 오른쪽 자식만 가짐을 의미하며 공백 노드도 자식 노드 취급
- 모든 노드의 차수가 2이하라 구현하기 편리
- 서브트리간에 순서가 존재 (왼,오)
- 일반 트리를 이진 트리로 바꾸기 위해서는 첫 자식 노드 간선만 남기고 나머지 간선을 제거 후 형제노드를 간선으로 연결한 후 시계 방향으로 45도 회전시키면 된다.
이진트리의 종류
- 포화이진트리 : 모든 레벨의 노드가 포화상태로 꽉 차 있는 트리, 높이가 h일 때 최대 노드 개수는 2^h - 1의 노드를 가진 이진트리이며 루트를 1번으로 하여 2^h -1까지 정해진 위치에 대한 노드 번호를 가진다.

- 완전이진트리 : 높이가 h일 때 레벨1부터 h-1까지는 노드가 모두 채워지며 마지막 레벨 h에서는 노드가 순서대로(중간에 빈 곳이 존재하면 x) 채워지고 높이가 h이고 노드 수가 n개일 때 (단, n < 2^h -1), 노드의 위치가 포화이진트리에서 노드 1번 ~ n번까지의 위치와 완전히 일치하는 트리이다. 하지만 n+1번부터 2^h -1번까지의 노드는 공백노드다

- 균형이진트리 : 모든 노드의 좌우 서브트리 높이 차이가 1이하인 트리
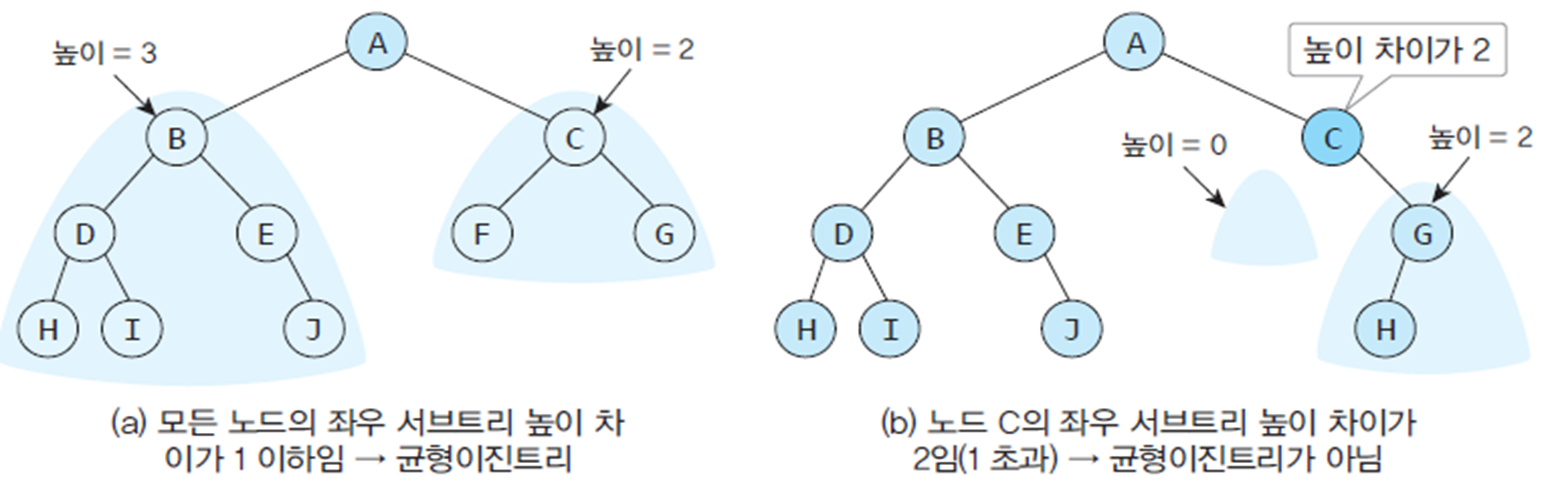
- 편향이진트리 : 높이가 h일 때 h개의 노드를 가지면서 모든 노드가 왼쪽이나 오른쪽 중 한방향으로만 서브트리를 가지고 있는 이진트리

이진트리의 특징
- 루트를 제외한 (n-1)개의 노드가 부모노드와 연결되는 한 개의 간선을 가지므로 노드의 개수가 n개 이면 간선의 개수는 n-1개이다.
- 높이가 h인 이진트리가 가질 수 있는 노드의 개수는 최소 h ~ 2^h -1개의 노드이다.
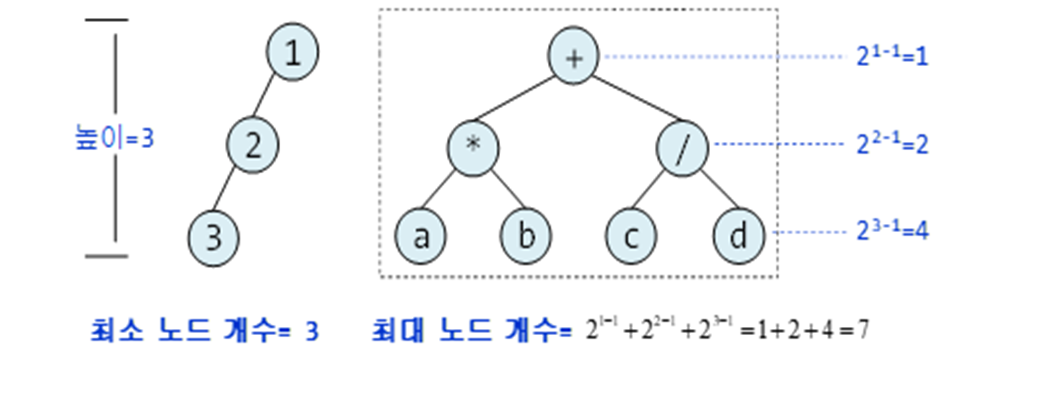
- n개 노드의 이진트리의 높이는 log2(n+1) ~ n이다
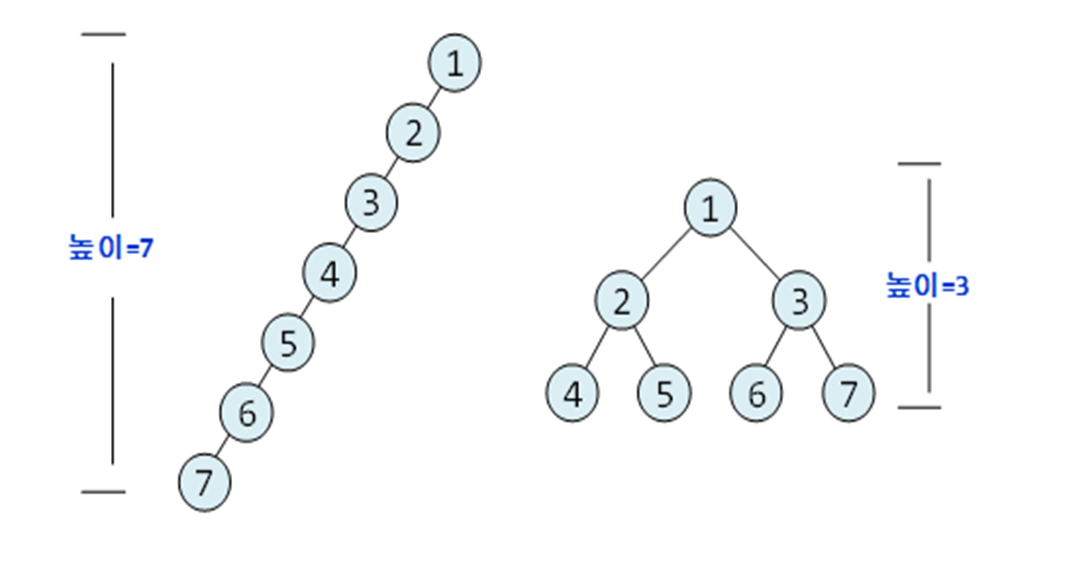
순회란?
- 트리의 모든 노드들을 체계적으로 한 번씩 방문하는 작업
- 선형자료구조에서의 순회는 하나의 방법만 존재
- 이진트리에서는 다양한 순회 방법이 존재(비선형자료구조이기에)
전위순회 : VLR로 출력
- 루트 -> 왼쪽 자식 -> 오른쪽 자식
중위순회 : LVR로 출력
- 왼쪽자식 -> 루트 -> 오른쪽 자식
후위순회 : LRV로 출력
- 왼쪽 자식 -> 오른쪽 자식 -> 루트
레벨순회 : 노드를 레벨 순으로 검사, 큐를 이용해 구현

탐색이란?
- 가장 중요한 컴퓨터 응용의 하나로, 레코드의 집합에서 특정한 레코드를 찾음
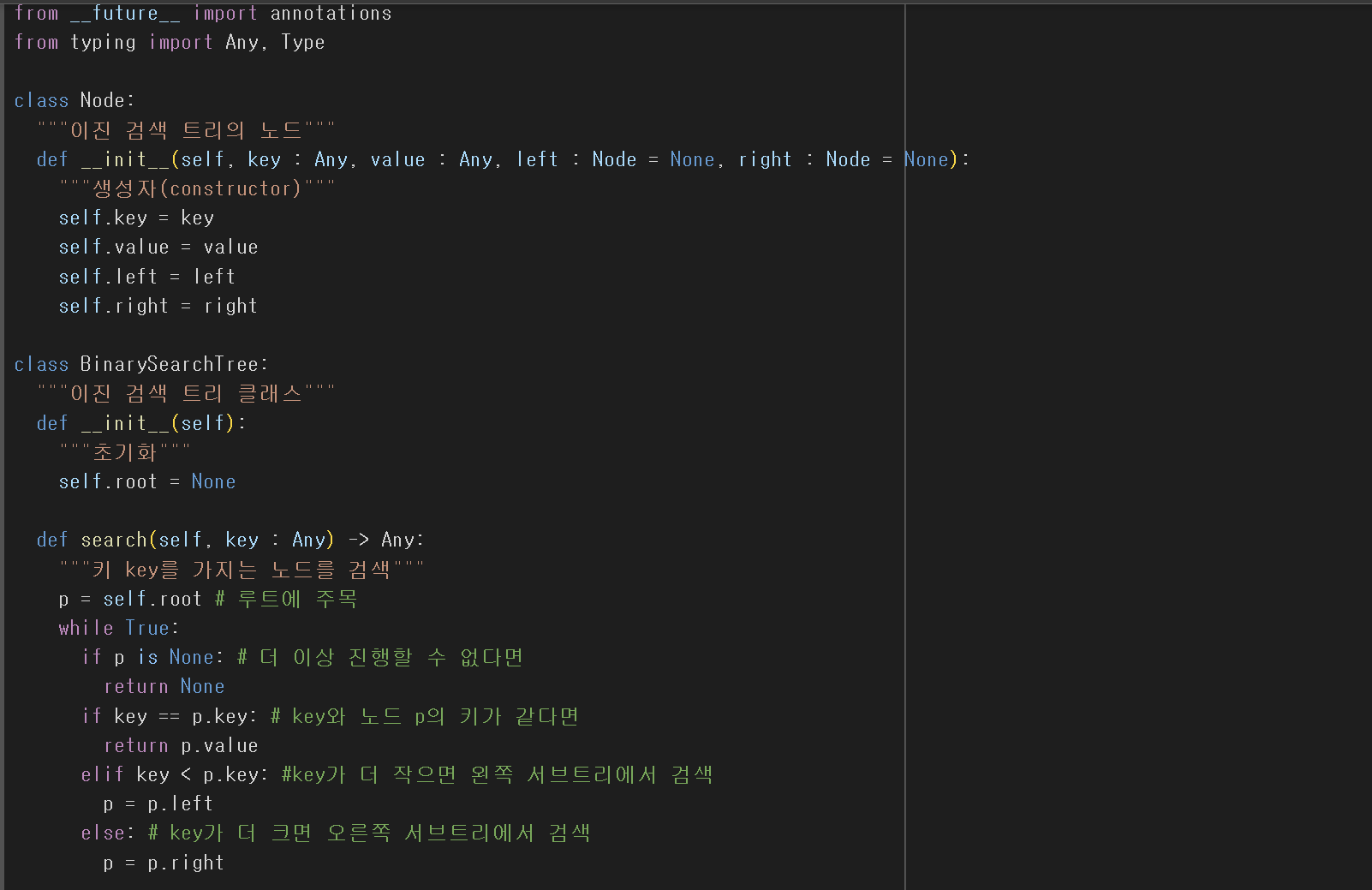
이진탐색트리란?
- 효율적인 탐색을 위한 이진트리 기반의 탐색을 위한 자료구조
- 모든 노드는 유일한 키여야 한다.
- 왼쪽 서브트리 키는 루트의 키보다 항상 작다.
- 오른쪽 서브트리의 키는 항상 루트의 키보다 크다.
- 왼쪽 서브트리와 오른쪽 서브트리도 이진탐색트리이다.
- 이 트리를 중위순회 하게 되면 오름차순으로 정렬된 값이 나온다.
- 위치를 지정하지 않고 노드 삽입/삭제 가능하다
- 탐색, 삽입, 삭제 연산의 시간복잡도는 높이가 h일 경우 O(h)이다. 즉 트리에 높이에 비례한다.
- n개의 노드를 가지는 이진탐색트리의 경우 일반적인 이진트리의 높이가 log2(n)이므로 이진탐색트리 연산 시간복잡도는 O(log2(n))이다.
- 포화이진트리(최선의경우) : O(log2(n)), 완전경사이진트리(최악의 경우) : O(n)
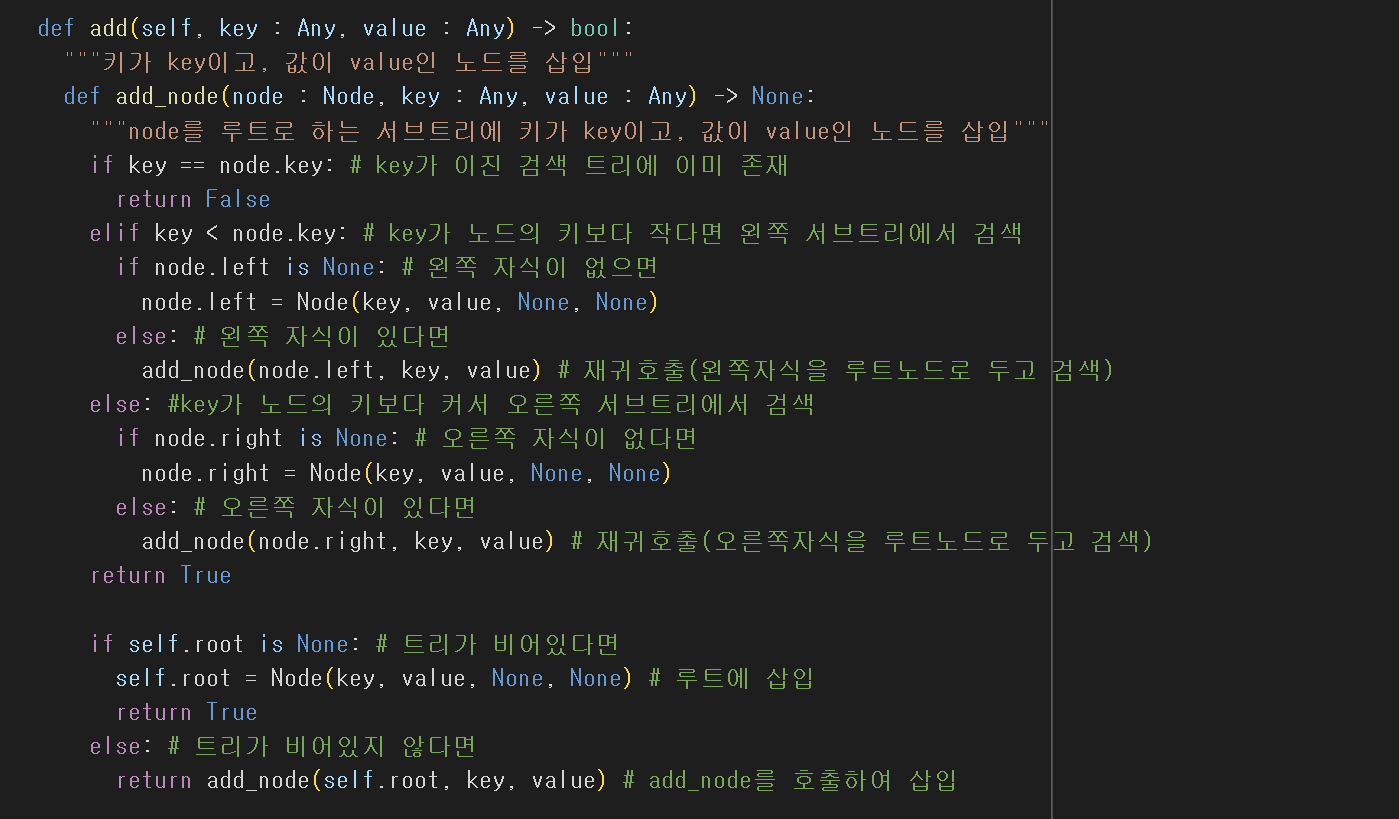
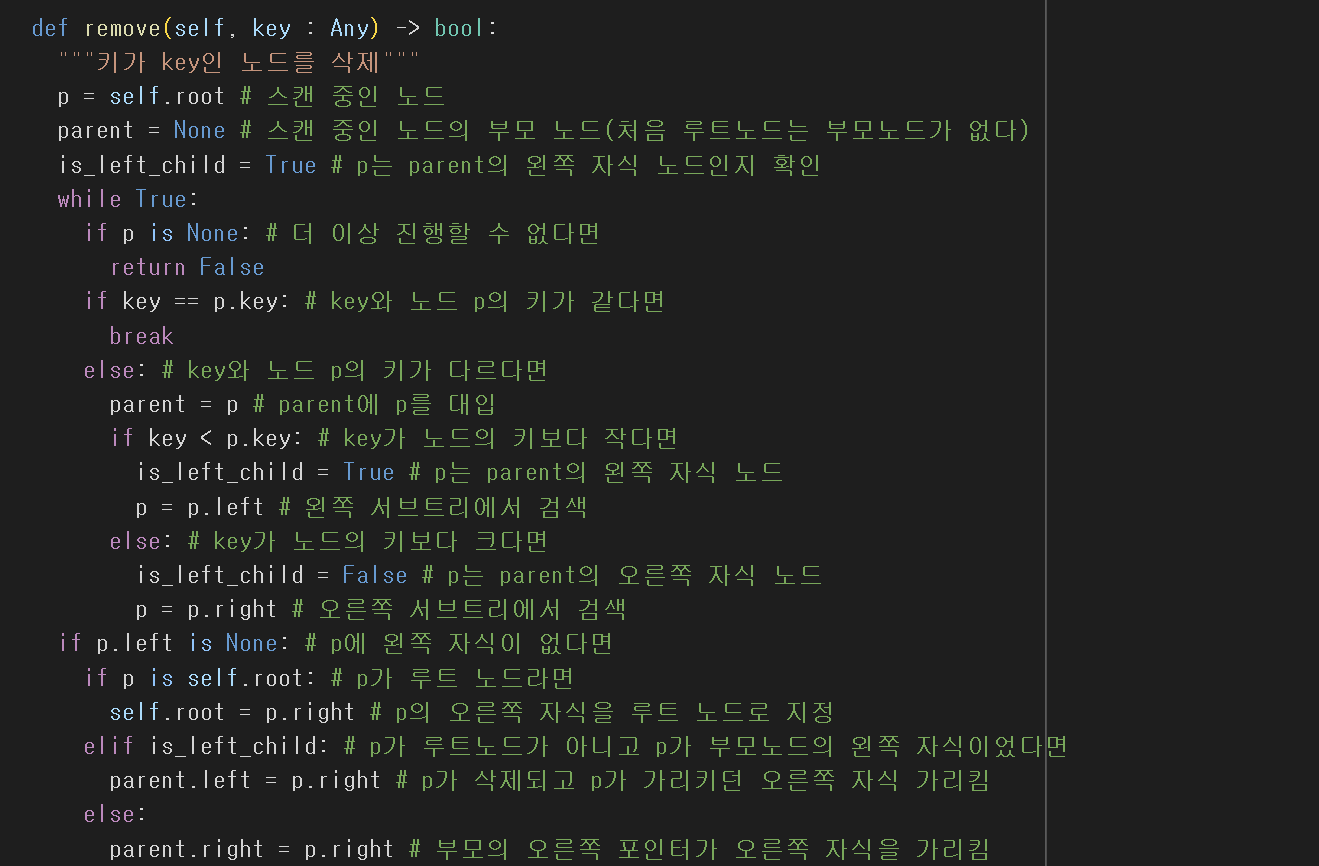

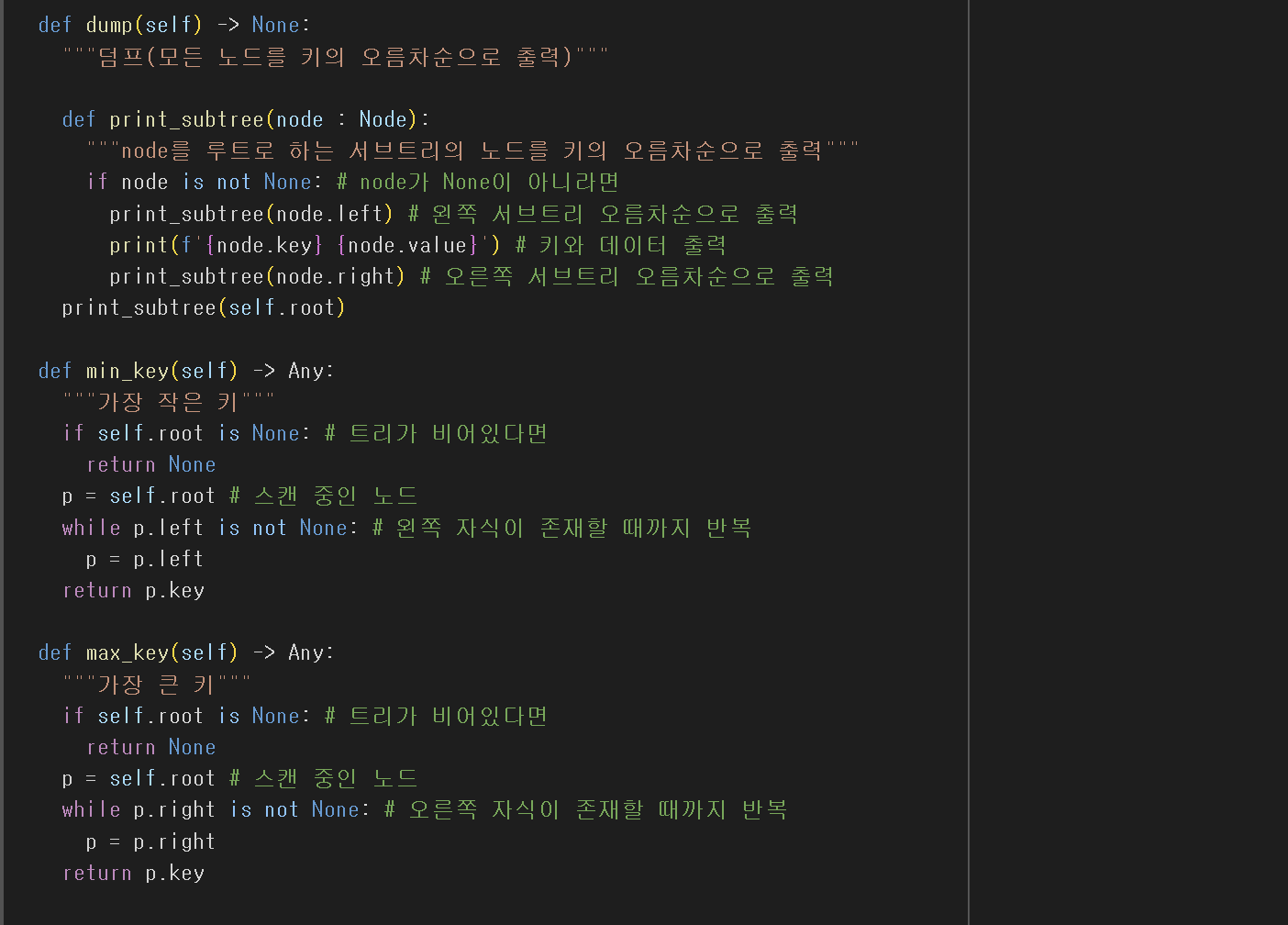
힙이란?
- 완전 이진트리의 일종, 빈곳이 없어 배열을 사용
- 킷값이 가장 큰 or 작은 노드를 빨리 찾을 수 있도록 설계
- 최대힙 : 부모의 킷값이 자식의 킷값보다 크거가 같은 완전이진트리
- 최소힙 : 부모의 킷값이 자식의 킷값보다 작거나 같은 완전이진트리
- 힙의 구조(완전이진트리구조), 크기조건(최대, 최소힙)을 만족해야함
- k의 부모 인덱스 : k/2, k의 왼쪽 자식 인덱스 : 2*k , k의 오른쪽 자식 인덱스 : 2*k + 1
- 우선순위큐라고 불리기도 한다.
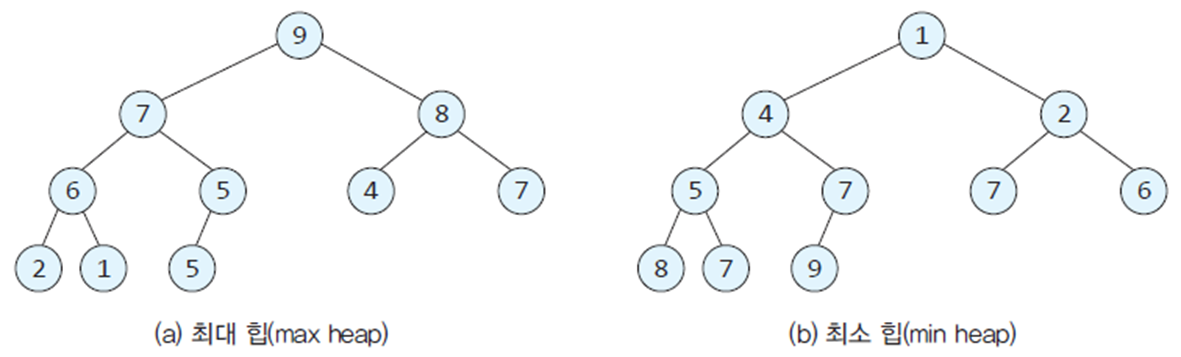

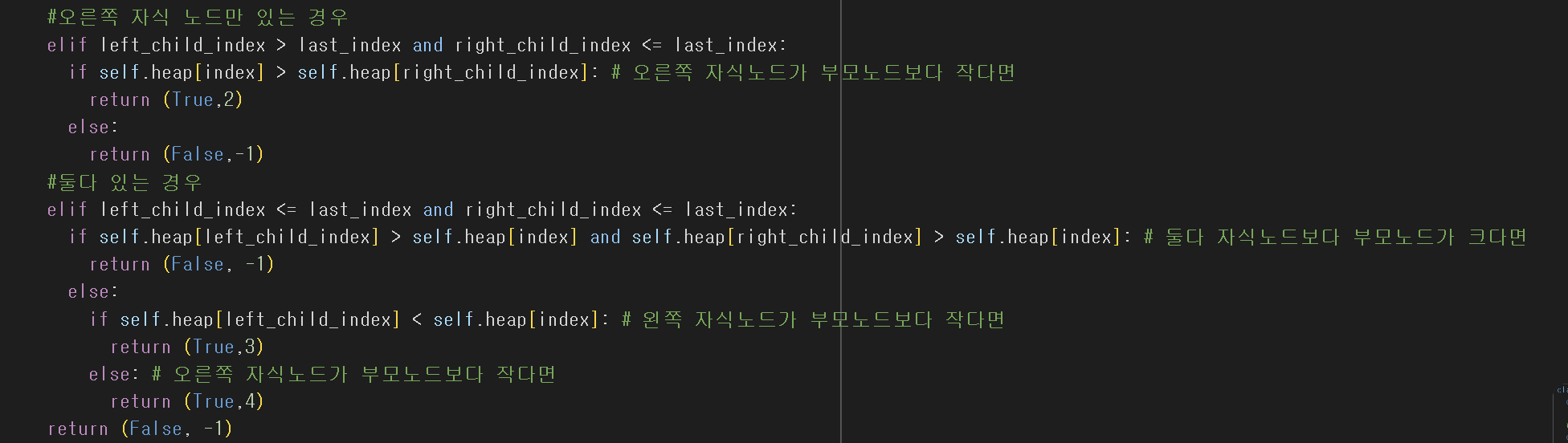
-여기서 둘다 있는 경우 첫번째 if문은 오른쪽, 왼쪽 자식노드가 부모노드보다 클경우이다. 주석 오타!
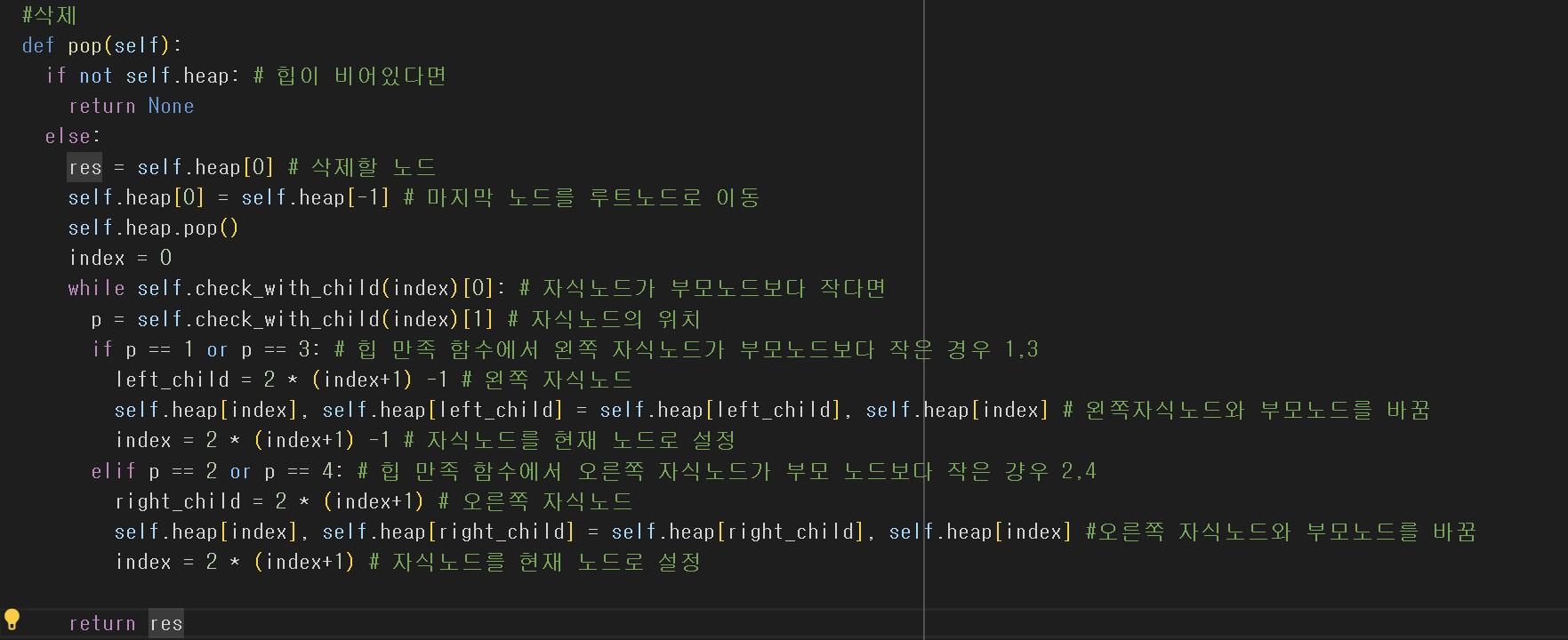
- 힙을 직접구현 할 수도 있지만 파이썬에서는 라이브러리를 제공하기 때문에 아래 사진은 라이브러리 사용한 것이다.
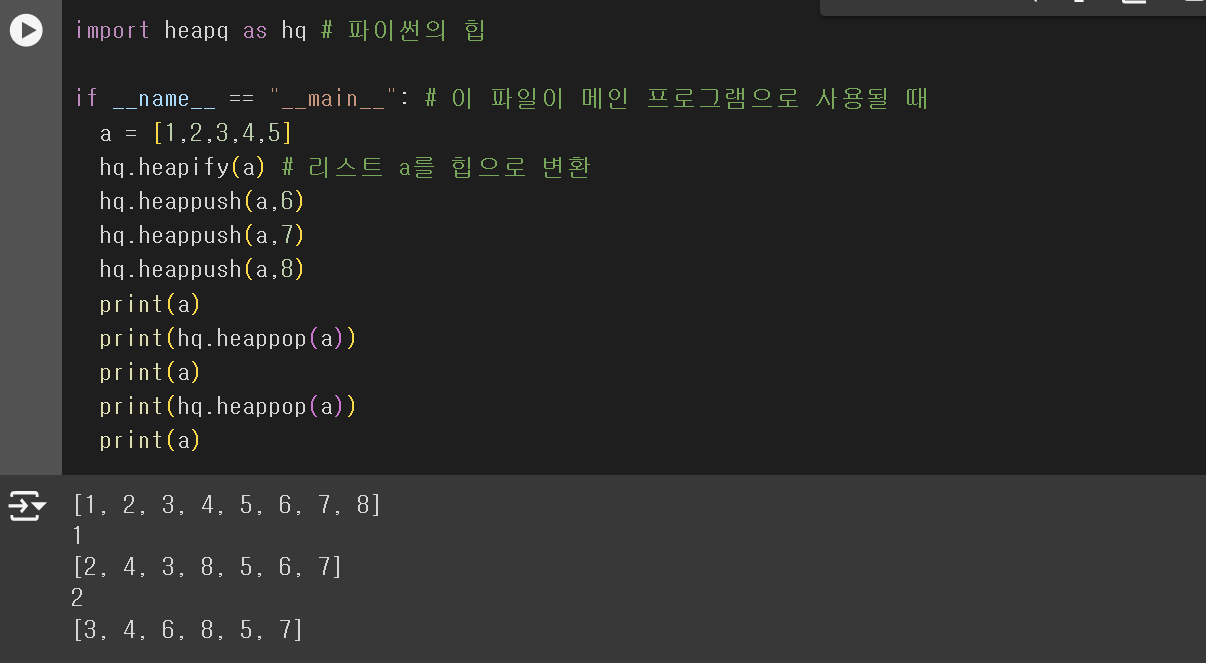
사진 출처:
쉽게 배우는 C 자료구조 | 생능출판사
코딩을 조금이라도 해 보았다면 프로그래밍이 자료(data)를 주로 다루는 것임을 알 수 있을 것이다. 우리가 프로그램을 개발할 때 가장 먼저 해야 할 일은 처리할 자료를 컴퓨터가 잘 다룰 수 있
www.booksr.co.kr